3% кислоты;x кг взято на смесь из 1-ого и 2-ого растворов;Масса кислоты в растворе - x * , но если перевести в десятичную дробь (что проще и удобнее в этой задаче), то получаем → x * 0,03 = 0,03x
2 раствор:
10% кислоты;(8,4 - x) кг - т.к следуя из условия задачи, смешав 1-ый и 2-ой растворы мы получим "3-ю смесь", масса которой = 8,4 кг. Значит нам надо вычитать из 3-ей смеси (раствора) x - массу 1-ого раствора, что сделано действием (8,4 - x) кг.Масса кислоты в растворе - 0,1 * (8,4 - x) кг. Поясняю → чтобы узнать массу кислоты в растворе надо умножить массу раствора на %-ое содержание кислоты в нём (что делалось с 1-ым раствором). ( Если кто не понял, почему надо именно умножать, то отдельное объяснение ждёт Вас в конце! )
3 раствор (смесь 1-ого и 2-ого растворов):
5% кислоты;Масса получившегося раствора (смеси) = 8,4 кг.Масса кислоты в растворе = 8,4 * (снова переведём в десятичную дробь, для удобства → 8,4 * 0,05 = 0,42 кгПерейдём к составлению уравнения!
Все данные нам известны. Т.к. алгебра с 7 класса начинается, мы знаем (ну должны наверное) уравнения... Да и по другому тут не решишь.
0,03x + 0,1(8,4 - x) = 0,42 кг (на месте между 0,03 и x; 0,1 и (8,4 - x) стоит умножение, обычно его не пишут в уже в 7 классе) (делаем так, чтобы получалась масса 5%-ов в смеси этих 2-ух растворов, а именно, приравниваем сумму масс кислоты в 1-ом и во 2-ом растворах к массе кислоты в смеси этих растворов.)Раскрываем скобки! → 0,03x + 0,84 - 0,1x = 0,42 кг.Теперь, переносим "+ 0,84" за скобки, изменяя знак → 0,03x - 0,1x = 0,42 - 0,84 кгПриводим подобные (многочлены) и считаем! → -0,07x = -0,42 кгТеперь, находим x (сколько взято для "3 раствора")! → x = -0,42 / -0.07 (деление).По правилам записи уравнений, записываем ещё строчку (после того как поделил) → x = 6 кг (результат положительный, т.к. при делении 2-ух отрицательных чисел, знак меняется на +).
Оуу, ее! Мы знаем сколько положили кг 1-ого раствора в смесь!
Теперь узнаем, сколько положили 2-ого → 8,4 - 6 = 2,4 кг.
Всё!!1 ответ: 1-ого раствора надо положить 6 кг, а 2-ого 2,4 кг.
А теперь, объяснение "Почему надо умножать именно на 0,1 * (8,4 - x)":
Если вспомнить проценты, то их можно приставить в виде дроби (6% → , 39% → и т.д.).
Значит. 10% = , сокращаем и получаем .
Должна промелькнуть мысль, что "3% от..." и она верна! Чтобы найди часть от числа (например, от 5, то нам надо 5 / 10 * 3 (5 разделить на 10 и уможить на 3, но дробь уже подрузамевает такое действие, так, что мы можем записать так (т.к. целое число можно перевести в неправильную дробь): , а если убрать 1 (т.к. она не изменит результат), то мы получим, то, что нам просто надо * 5 (умножить на 5), а если вместо 5 поставить x, то было бы тоже самое (т.к x можно представить как ) → → * x = x.
1 час 45 минут = 105 мин
1 час 15 минут = 75 мин
2 час 55 минут = 175 мин
Пусть 1 - объем всего бассейна;
x - производительность первой трубы;
y - производительность второй трубы;
z - производительность третьей трубы;
t - производительность четвертой трубы
1) По условию первая, вторая и третья трубы наполняют бассейн за 105минут, значит, их совместная производительность равна:
2) Аналогично находим совместную производительность первой, второй и четвёртой труб:
3) Находим совместную производительность третьей и четвёртой труб:
Сложим полученные уравнения:
И, наконец, получим время, за которое заполнится бассейн, если открыть все 4 трубы:
ответ: 70 мин= 1 ч 10 мин
(это автор вопроса, с другого аккаунта)
1 раствор:
3% кислоты;x кг взято на смесь из 1-ого и 2-ого растворов;Масса кислоты в растворе - x *2 раствор:
10% кислоты;(8,4 - x) кг - т.к следуя из условия задачи, смешав 1-ый и 2-ой растворы мы получим "3-ю смесь", масса которой = 8,4 кг. Значит нам надо вычитать из 3-ей смеси (раствора) x - массу 1-ого раствора, что сделано действием (8,4 - x) кг.Масса кислоты в растворе - 0,1 * (8,4 - x) кг. Поясняю → чтобы узнать массу кислоты в растворе надо умножить массу раствора на %-ое содержание кислоты в нём (что делалось с 1-ым раствором). ( Если кто не понял, почему надо именно умножать, то отдельное объяснение ждёт Вас в конце! )3 раствор (смесь 1-ого и 2-ого растворов):
5% кислоты;Масса получившегося раствора (смеси) = 8,4 кг.Масса кислоты в растворе = 8,4 *Все данные нам известны. Т.к. алгебра с 7 класса начинается, мы знаем (ну должны наверное) уравнения... Да и по другому тут не решишь.
0,03x + 0,1(8,4 - x) = 0,42 кг (на месте между 0,03 и x; 0,1 и (8,4 - x) стоит умножение, обычно его не пишут в уже в 7 классе) (делаем так, чтобы получалась масса 5%-ов в смеси этих 2-ух растворов, а именно, приравниваем сумму масс кислоты в 1-ом и во 2-ом растворах к массе кислоты в смеси этих растворов.)Раскрываем скобки! → 0,03x + 0,84 - 0,1x = 0,42 кг.Теперь, переносим "+ 0,84" за скобки, изменяя знак → 0,03x - 0,1x = 0,42 - 0,84 кгПриводим подобные (многочлены) и считаем! → -0,07x = -0,42 кгТеперь, находим x (сколько взято для "3 раствора")! → x = -0,42 / -0.07 (деление).По правилам записи уравнений, записываем ещё строчку (после того как поделил) → x = 6 кг (результат положительный, т.к. при делении 2-ух отрицательных чисел, знак меняется на +).Оуу, ее! Мы знаем сколько положили кг 1-ого раствора в смесь!
Теперь узнаем, сколько положили 2-ого → 8,4 - 6 = 2,4 кг.
Всё!!1 ответ: 1-ого раствора надо положить 6 кг, а 2-ого 2,4 кг.
А теперь, объяснение "Почему надо умножать именно на 0,1 * (8,4 - x)":
Если вспомнить проценты, то их можно приставить в виде дроби (6% →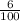 , 39% →
, 39% → 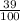 и т.д.).
и т.д.).
Значит. 10% =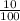 , сокращаем и получаем
, сокращаем и получаем 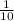 .
.
Должна промелькнуть мысль, что "3% от..." и она верна! Чтобы найди часть от числа (например,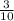 от 5, то нам надо 5 / 10 * 3 (5 разделить на 10 и уможить на 3, но дробь уже подрузамевает такое действие, так, что мы можем записать так (т.к. целое число можно перевести в неправильную дробь):
от 5, то нам надо 5 / 10 * 3 (5 разделить на 10 и уможить на 3, но дробь уже подрузамевает такое действие, так, что мы можем записать так (т.к. целое число можно перевести в неправильную дробь): 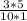 , а если убрать 1 (т.к. она не изменит результат), то мы получим, то, что нам просто надо
, а если убрать 1 (т.к. она не изменит результат), то мы получим, то, что нам просто надо 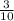 * 5 (умножить на 5), а если вместо 5 поставить x, то было бы тоже самое (т.к x можно представить как
* 5 (умножить на 5), а если вместо 5 поставить x, то было бы тоже самое (т.к x можно представить как 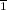 ) →
) → 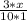 →
→ 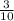 * x =
* x = 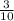 x.
x.