Представим первое число как X
Второе как X + 5
Составим уравнение и решим его.
x * (x+5) = 24
x² + 5x = 24
x² + 5x - 24 = 0
(a = 1; b = 5; c = -24.)
D = b² - 4ac
D = 5² - 4 * 1 * (-24)
D = 25 + 96
D = 121
x₁₂ =
- первое число подходит, т.к положительное;
- число не подходит, т.к отрицательное.
Подставим первое число в условие X+5
⇒ x + 5 = 3 + 5 = 8 - второе число.
Произведение двух найденных чисел равно 24:
3 * 8 = 24
Одно число больше другого на 5:
8 - 5 = 3 - первое число;
3 + 5 = 8 - второе число;
ответ: Первое число 3, второе число 8.
В решении.
Объяснение:
Нужно изучить свойства корней.
а) (2√5 + 3√2)(√5 - √8)=
=(2√5 + 3√2)(√5 - √4*2)=
=(2√5 + 3√2)(√5 - 2√2)=
умножить каждый член первых скобок на каждый член вторых скобок:
=2√5 * √5 + 3√2 * √5 - 2√5 * 2√2 - 3√2 * 2√2 =
= 2 * 5 + 3√10 - 4√10 -6 * 2 =
=10 - 12 - √10 =
= -2 - √10;
б) (√11 - 0,5√22)(0,5√22 + √11) =
=√11*0,5√22 + √11*√11 - 0,5√22*0,5√22 - 0,5√22*√11 =
=0,5√242 + 11 - 0,5*22 - 0,5√242 =
=0,5√242 + 11 - 11 - 0,5√242 =
=0 (все члены выражения взаимно уничтожаются).
в) (√42)² - (2√6 - 3√2)²=
вторые скобки квадрат разности, по формуле сокращённого умножения:
=42 - [(2√6)² - 2*2√6*3√2 + (3√2)²]=
=42 - (4*6 -12√12 + 9*2)=
=42 - (24 - 12√4*3 + 18)=
=42 - (24 - 12*2√3 + 18)=
=42 - (42 - 24√3)=
=42 - 42 + 24√3=
=24√3.
Представим первое число как X
Второе как X + 5
Составим уравнение и решим его.
x * (x+5) = 24
x² + 5x = 24
x² + 5x - 24 = 0
(a = 1; b = 5; c = -24.)
D = b² - 4ac
D = 5² - 4 * 1 * (-24)
D = 25 + 96
D = 121
x₁₂ =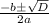
Подставим первое число в условие X+5
⇒ x + 5 = 3 + 5 = 8 - второе число.
Произведение двух найденных чисел равно 24:
3 * 8 = 24
Одно число больше другого на 5:
8 - 5 = 3 - первое число;
3 + 5 = 8 - второе число;
ответ: Первое число 3, второе число 8.
В решении.
Объяснение:
Нужно изучить свойства корней.
а) (2√5 + 3√2)(√5 - √8)=
=(2√5 + 3√2)(√5 - √4*2)=
=(2√5 + 3√2)(√5 - 2√2)=
умножить каждый член первых скобок на каждый член вторых скобок:
=2√5 * √5 + 3√2 * √5 - 2√5 * 2√2 - 3√2 * 2√2 =
= 2 * 5 + 3√10 - 4√10 -6 * 2 =
=10 - 12 - √10 =
= -2 - √10;
б) (√11 - 0,5√22)(0,5√22 + √11) =
умножить каждый член первых скобок на каждый член вторых скобок:
=√11*0,5√22 + √11*√11 - 0,5√22*0,5√22 - 0,5√22*√11 =
=0,5√242 + 11 - 0,5*22 - 0,5√242 =
=0,5√242 + 11 - 11 - 0,5√242 =
=0 (все члены выражения взаимно уничтожаются).
в) (√42)² - (2√6 - 3√2)²=
вторые скобки квадрат разности, по формуле сокращённого умножения:
=42 - [(2√6)² - 2*2√6*3√2 + (3√2)²]=
=42 - (4*6 -12√12 + 9*2)=
=42 - (24 - 12√4*3 + 18)=
=42 - (24 - 12*2√3 + 18)=
=42 - (42 - 24√3)=
=42 - 42 + 24√3=
=24√3.