Я прикрепил фото того, как выглядит график. А сейчас разберемся как его строить.
Для начала давай раскроем скобки:
y = (2x - 6)(x + 1) //внесли двойку
y = x*(2x - 6) + (2x - 6) //раскрыли вторую скобку
y = 2x^2 - 6x + 2x - 6
y = 2x^2 - 4x - 6
Теперь можно решать по разному. Если хочешь напишу ещё
А пока воспользуемся самым действенным
Примем x0 и y0 за координаты вершины параболы.
Тогда , а (вторую формулу если что можно не запоминать, можешь просто подставить в уравнение полученное x0)
И так
Значит
Теперь может просто подставлять значения. Но в данном случае можешь схитрить.
Так как изначальное уравнение выглядело как y = 2(x - 3)(x + 1), то если присмотреться, то можно заметить, что эта парабола пересекает ось x в точках 3 и -1. Но самое интересное это коэффициент 2. Ты можешь просто квадраты x умножать на два и получать желанную точку. После просмотра второй картинки, мои слова станут более понятны
Я прикрепил фото того, как выглядит график. А сейчас разберемся как его строить.
Для начала давай раскроем скобки:
y = (2x - 6)(x + 1) //внесли двойку
y = x*(2x - 6) + (2x - 6) //раскрыли вторую скобку
y = 2x^2 - 6x + 2x - 6
y = 2x^2 - 4x - 6
Теперь можно решать по разному. Если хочешь напишу ещё
А пока воспользуемся самым действенным
Примем x0 и y0 за координаты вершины параболы.
Тогд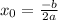а
, а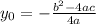 
(вторую формулу если что можно не запоминать, можешь просто подставить в уравнение полученное x0)
И так
Значит
Теперь может просто подставлять значения. Но в данном случае можешь схитрить.
Так как изначальное уравнение выглядело как y = 2(x - 3)(x + 1), то если присмотреться, то можно заметить, что эта парабола пересекает ось x в точках 3 и -1. Но самое интересное это коэффициент 2. Ты можешь просто квадраты x умножать на два и получать желанную точку. После просмотра второй картинки, мои слова станут более понятны
Объяснение:
1. -х² - 4х + 4k = 0.
Для удобства разделим обе части на -1:
х² + 4х - 4k = 0.
Уравнение - квадратное. Найдем его дискриминант.
D = b² - 4ac = 4² - 4 × 1 × (-4k) = 16 + 16k.
Рассмотрим 3 возможных случая:
1) D < 0. Если D < 0, то корней нет:
16 + 16k < 0; 16k < -16 => k < -1. При k < -1 корней уравнение не имеет.
2) D = 0; 16 + 16k = 0 => k = -1. При таком значении параметра уравнение имеет единственный корень x = -b/2a = -4/(2×1)=-2.
3) D > 0. Если D > 0, (k>-1) то уравнение имеет два корня. Дальнейшее объяснение в первом вложении.
ответ: при k < -1 корней нет; при k = -1 корень x = -2; при k > -1 корни: х1 = -2 + 2√(k+1), х2 = -2 - 2√(k + 1).
2. Полное решение во втором вложении (решения справедливы для любого значения параметра k)