№1. Решить уравнение.
Домножим левую и правую часть уравнения на .
Получим:
Обратите внимание на то, что корень не подходит.
Почему? Давайте посмотрим на знаменатель исходного уравнения: . Если мы подставим , то получим , а на 0 делить нельзя.
ответ: x =
№2. Решить уравнение.
Общий знаменатель в левой части - это .
ответ: x₁ = , x₂ =
№3. Решить уравнение.
Получаем, что - любое число.
ответ: - любое число.
№4. Решить задачу.
Пусть км/ч - собственная скорость лодки, тогда скорость по течению реки равна км/ч, а против течения км/ч.
Составим уравнение:
Так как скорость не может быть отрицательной, то отсеиваем корень .
Таким образом, получаем, что км/ч - собственная скорость лодки.
Значит, скорость лодки против течения равна км/ч
ответ: км/ч.
Успехов.
Раскрываем: sin2x = 2*sinx*cosx.
-2cos(x-π) = -2cos(π-x) = +2cosx.
Подставляем: 2*sinx*cosx + √2*sinx = √2 + 2cosx.
В левой части вынесем за скобки sinx:
sinx(2cosx + √2) = 2cosx + √2.
Правую часть перенесём влево и вынесем её за скобки.
(2cosx + √2)(sinx - 1) = 0.
Отсюда имеем:
2cosx + √2 = 0,
cosx = -√2/2, x = 2πk +- (3π/4), k ∈ Z.
sinx - 1 = 0.
sinx = 1, x = (π/2) + 2πk, k ∈ Z.
На заданном промежутке [π; (5π/2)] есть только 2 решения:
х = (5π/4) и х = 5π/2).
№1. Решить уравнение.
Домножим левую и правую часть уравнения на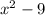 .
.
Получим:
Обратите внимание на то, что корень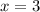 не подходит.
не подходит.
Почему? Давайте посмотрим на знаменатель исходного уравнения: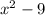 . Если мы подставим
. Если мы подставим 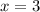 , то получим
, то получим 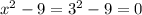 , а на 0 делить нельзя.
, а на 0 делить нельзя.
ответ: x =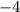
№2. Решить уравнение.
Общий знаменатель в левой части - это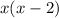 .
.
ответ: x₁ =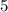 , x₂ =
, x₂ = 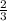
№3. Решить уравнение.
Общий знаменатель в левой части - это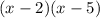 .
.
Получаем, что - любое число.
- любое число.
ответ: - любое число.
- любое число.
№4. Решить задачу.
Пусть км/ч - собственная скорость лодки, тогда скорость по течению реки равна
км/ч - собственная скорость лодки, тогда скорость по течению реки равна 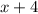 км/ч, а против течения
км/ч, а против течения 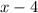 км/ч.
км/ч.
Составим уравнение:
Так как скорость не может быть отрицательной, то отсеиваем корень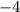 .
.
Таким образом, получаем, что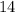 км/ч - собственная скорость лодки.
км/ч - собственная скорость лодки.
Значит, скорость лодки против течения равна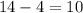 км/ч
км/ч
ответ: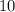 км/ч.
км/ч.
Успехов.