Модуль «реальная » в таблице нормативы по прыжкам в длину с места для 11 класса. мальчики мальчики мальчики девочки девочки девочки отметка «3» «4» «5» «3» «4» «5» дальность (в см) 200 220 230 155 170 185 какую отметку получит мальчик, прыгнувший на 215 см? в ответе укажите номер правильного варианта. 1) неудовлетворительно 2) «3» 3) «4» 4) «5» при резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. на рисунке показан график этой зависимости (для сухой асфальтовой дороги). по горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). определите по графику, с какой скоростью двигался автомобиль, если его тормозной путь составил 50 метров. ответ дайте в километрах в час. hello_html_42feacb5.png какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5%-ной скидкой? на клетчатой бумаге с размером клетки 1см x 1см отмечены точки а, в и с. найдите расстояние от точки а до середины отрезка вс. ответ выразите в сантиметрах. hello_html_17f7dfdf.png 18. на диаграмме показано содержание питательных веществ в молочном шоколаде. определите по диаграмме, содержание каких веществ преобладает. *-к прочему относятся вода, витамины и минеральные вещества. 1) жиры 2) белки 3) углеводы 4) прочее в ответе запишите номер выбранного утверждения. hello_html_m2513a2b2.png 19. на экзамене 25 билетов, сергей не выучил 3 из них. найдите вероятность того, что ему попадётся выученный билет. 20. в фирме «родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле c=6000+4100n, где n — число колец, установленных в колодце. пользуясь этой формулой, рассчитайте стоимость колодца из 5 колец. ответ дайте в рублях. не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Дано:
Найти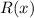
- остаток от деления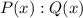 
Решение.
1) Для начала разложим многочлен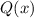
на множители, для этого решим уравнение:
2) Так как данный многочлен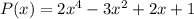
делится на 
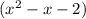с остатком, то представим его в виде
где
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
3) Подставим в равенство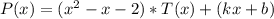
первый корень 
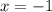и получим:
Вычислим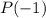
.
Так как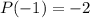
, то
4) Аналогично решаем и со вторым корнем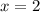
.
5) Подставим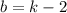
в полученное уравнение:
6)
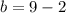
ответ: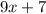
|x-1| + |x-a| = 1 - a
Сразу заметим, что левая часть ≥ 0, значит и правая часть должна будет тоже быть ≥ 0 :
1 - a ≥ 0
a ≤ 1
Теперь может найти подмодульные нули :
1) x - 1 = 0 2) x - a = 0
x = 1 x = a
Выставим их на числовой прямой и заметим, что а будет находиться сзади 1, так как мы выяснили что а ≤ 1, а при а = 1 есть только один корень :
x < a a ≤ x < 1 x ≥ 1
(a)(1)
Рассмотри три случая :
1) x < a
-x + 1 - x + a = 1 - a
-2x + 2a = 0
2(a - x) = 0
x = a - не подходит, т.к x < a
ответ : x ∈ ∅
2) a ≤ x < 1
-x + 1 + x - a = 1 - a
0 = 0
x ∈ R
ответ : x ∈ [a ; 1)
3) x ≥ 1
x - 1 + x - a = 1 - a
2x = 2
x = 1
ответ : x = 1
Соединим все наши решения :
[ x ∈ ∅
[ x ∈ [a ; 1)
[ x = 1
x ∈ [a ; 1]
Уравнение будет иметь ровно 3 целых решения, если а = -1.
Уравнение будет иметь 3 и больше решений при а ≤ -1