- квадратное уравнение относительно p; в принципе можно решать с дискриминанта, но числа не самые простые, поэтому идти по этому пути лень. Пытаемся угадать одно из решений и без труда его находим: p=1. Дальнейшее элементарно: по теореме Виета произведение корней равно 28-4x, а раз первый корень p=1, то второй равен p=28-4x.
1-й случай
2-й случай.
Решение x= 3 легко угадывается (8=8), других решений быть не может, поскольку функция, стоящая в левой части уравнения, возрастает, а функция, стоящая в правой части уравнения, убывает.
домножим уравнение на 4 и сделаем замену 2t=p>0:
1-й случай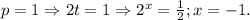
2-й случай.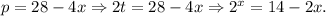
Решение x= 3 легко угадывается (8=8), других решений быть не может, поскольку функция, стоящая в левой части уравнения, возрастает, а функция, стоящая в правой части уравнения, убывает.
ответ: - 1; 3
х-пропускает вторая
х+1200 -пропускает первая
30мин=0,5ч
12м³=12000л
12000/х-12000/(х+1200)=0,5
12000/х-12000/(х+1200)-0,5=0 умножим на х(х+1200)
12000(х+1200)-12000х-0,5х(х+1200)=0
12000х+14400000-12000х-0,5х²-600х=0
-0,5х²-600х+14400000=0
х²+1200х-28800000=0
D = 1200² - 4·1·(-28800000) = 1440000 + 115200000 = 116640000
x1=(-1200-√116640000)/(2*1)=(-1200-10800)/2 = -12000/2 = -6000-не подходит
x2=(-1200+√116640000)/(2*1)=(-1200+10800)/2 = 9600/2 = 4800 л/час=80л/мин-вторая
4800+1200=6000л/ч=100л/мин-первая