Мой вопрос связан не с решение какого-либо задания, а с его объяснением. По какому принципу решается данное уравнение я знаю и, более того, понимаю. Однако есть единственная вещь, которую я, спустя долгое время, так и не смогла понять: куда девается знаменатель? То есть мне не раз говорили, что знаменатель просто отбрасывается,а мы работаем с числителем, НО! У меня в связи с этим есть наводящий вопрос: с каких пор в математике (подчеркиваю это слово) можно просто взять и отбросить знаменатель и решать без него. Просто взять и отбросить целое число (или цифру). Почему такое возможно, если все время нам твердили, что в математике важно все! По какому принципу мы просто решаем и в один момент такие "а ну, будем решать без знаменателя" и все? Вот, допустим,когда мы решаем дроби, мы делаем следующее: *сокращение учитывать не будем* Ну так вот. Решая этот незамысловатый пример, МЫ ЖЕ НЕ ОТБРАСЫВАЕМ ПОЛУЧЕННЫЙ НАМИ ЗНАМЕНАТЕЛЬ 10. Потому что будь так, мы бы получили ответ просто 4. Но нет, знаменатель здесь остается и никуда не девается. Так почему же это происходит в тех уравнениях? Заранее за ответ, это бы мне очень ! (надеюсь на развернутое и понятное объяснение)
Исследуем знак второй производной: f''(x)=0 - когда где
Поскольку a³≤a², b³≤b², причем при a∈(0,1); b∈(0,1) неравенства строгие, делаем вывод, что такое возможно только при a=1; b=0 или a=0; b=1, при прочих a и b, удовлетворяющих второму уравнению, сумма их кубов будет меньше 1, откуда вторая производная всюду неотрицательна, то есть функция вогнута. А поскольку других решений на промежутке нет.
2) уравнение принимает вид
На этом участке подобное рассуждение не проходит; кроме x=2 точно есть корень слева от нуля, поскольку f(0)>6. Будем рассуждать иначе.
уравнение превращается в
Обе части положительны, смело возводим в квадрат (а можно было и к половинному углу свести):
6-6cos 2t-10sin 2t+2sin 2t cos 2t=0;
12sin² t-20 sin t cos t+4sin t cos t(cos² t-sin² t)=0; sin t=0 (⇒ a=0; b =2; x=2) или 3 sin t-5cos t+cos³ t-cos t sin² t=0;
(3sin t-5cos t)(cos²t+sin²t)+cos³ t-cos t sin^2 t=0;
3sin³t-6sin²t cos t+3sin t cos²t-4cos³ t=0; очевидно cos t≠0; tg t=p;
3p³-6p²+3p-4=0; домножаем на 9 и замена 3p=q: q³-6q+9q-36=0;
(q-2)³-3(q-2)-34=0;
но
Вот этот корень мы и искали. Подставлять найденное p для выписывания b, а затем x, сил уже не осталось.
Возможно, я где-то ошибся, но ошибку пока не вижу. Засим разрешите откланяться.
Смотря, какие звездочки красные, а какие белые. 1) Если площади красных 9 и 17, а белых 2 и 4, и мы клеим белые поверх красных, то площадь красной части: 9+17-2-4 = 20 2) А если наоборот, 2 и 4 красные, и мы их клеим поверх белых 9 и 17, то площадь красной части 2+4=6. Точно также можно рассмотреть другие варианты: 3) Красные 4 и 17, белые 9 на 17, и 2 на 4, площадь 4+17-2-9=10. 4) Красные 4 и 17, белые 9 под 4 и 2 на 17, площадь 4+17-2=19 И так далее в разных комбинациях, смотря, какая звезда какого цвета, и какая на какую наклеена.
Угадываем корни 2 и - 2. Заметим, что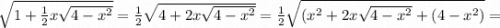
1) уравнение принимает вид
уравнение принимает вид
Исследуем знак второй производной: f''(x)=0 - когда где
где
2) уравнение принимает вид
уравнение принимает вид
На этом участке подобное рассуждение не проходит; кроме x=2 точно есть корень слева от нуля, поскольку f(0)>6. Будем рассуждать иначе.
Обе части положительны, смело возводим в квадрат (а можно было и к половинному углу свести):
6-6cos 2t-10sin 2t+2sin 2t cos 2t=0;
12sin² t-20 sin t cos t+4sin t cos t(cos² t-sin² t)=0; sin t=0 (⇒ a=0; b =2; x=2) или 3 sin t-5cos t+cos³ t-cos t sin² t=0;
(3sin t-5cos t)(cos²t+sin²t)+cos³ t-cos t sin^2 t=0;
3sin³t-6sin²t cos t+3sin t cos²t-4cos³ t=0; очевидно cos t≠0; tg t=p;
3p³-6p²+3p-4=0; домножаем на 9 и замена 3p=q: q³-6q+9q-36=0;
(q-2)³-3(q-2)-34=0;

Вот этот корень мы и искали. Подставлять найденное p для выписывания b, а затем x, сил уже не осталось.
Возможно, я где-то ошибся, но ошибку пока не вижу. Засим разрешите откланяться.
1) Если площади красных 9 и 17, а белых 2 и 4, и мы клеим белые поверх красных, то площадь красной части:
9+17-2-4 = 20
2) А если наоборот, 2 и 4 красные, и мы их клеим поверх белых 9 и 17, то площадь красной части 2+4=6.
Точно также можно рассмотреть другие варианты:
3) Красные 4 и 17, белые 9 на 17, и 2 на 4, площадь 4+17-2-9=10.
4) Красные 4 и 17, белые 9 под 4 и 2 на 17, площадь 4+17-2=19
И так далее в разных комбинациях, смотря, какая звезда какого цвета, и какая на какую наклеена.