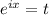Да, приведу самый простой пример:
Очевидно, что действительных решений тут нет.
Попробуем найти комплексные:
Сделаем замену :
Да, приведу самый простой пример:
Очевидно, что действительных решений тут нет.
Попробуем найти комплексные:
Сделаем замену :