Для того, чтобы назвать модель математической, необходимо наличие трех вещей:
1) Ввести переменные
2) задать область, на которой будет рассмотрена задача
3) составить функцию цели. т.е. определить, как решать поставленную условием задачу.
Переменные берем из вопроса. Что надо найти? скорость каждого автомобиля. Поэтому введем переменные v₁ и v₂ - скорости первого и второго автомобилей соответственно.
Обе переменные больше нуля.
Расстояние можно найти, если знаем время и скорость. кратко запишем условие с таблицы.
s v t
1 автомобиль 180км ?v₁ 1ч.36мн=1 .6ч/после встречи/
2 автомобиль 180км ?v₂ 2ч 30 мин.=2.5ч/после встречи/
Расстояние Время
До встречи После встречи скорость до после
1 х 180-х v₁ одинак. 1.6
2 180-х х v₂ одинак. 2.5
Пусть первый до встречи проехал х км, тогда второй (180-х) км.
До встречи затратили одно и то же время, т.к. вышли одновременно.
х/v₁=(180-х)/ v₂
v₁1.6+ v₂*2.5=180
Составлена система двух уравнений с двумя переменными. Собственно цель - найти переменные - значения скоростей. После решения системы выполнить отбор полученных решений и записать ответ.
Поскольку, любое уравнение можно поделить на его старший коэффициент, то будем считать, для удобства, что мы рассматриваем два приведенных кубических уравнения с рациональными коэффициентами.
, - рациональные числа.
Поскольку, данные уравнения имеют общий корень, то уравнение, являющееся их разностью, тоже содержит этот корень:
, поскольку коэффициенты уравнений непропорциональны, то все коэффициенты полученного квадратного уравнения ненулевые.
А значит, данный общий иррациональный корень принимает вид : , где - рациональные числа, при этом не полный квадрат, отсюда в частности .
Попробуем показать, что если корень уравнения
, то и корень данного уравнения , и наоборот. Сделаем некоторое упрощение.
Если число является корнем данного уравнения , то сделаем замену: , тогда после раскрытия скобок данное уравнение так же будет с рациональными коэффициентами и будет иметь корень
Такое уравнение примет вид :
, - рациональные числа.
Учитывая, что
Предположим, что , но тогда , учитывая, что - не полный квадрат, то левая часть равенства иррациональна, а правая рациональна, что невозможно. То есть мы пришли к противоречию, а значит :
Таким образом:
Аналогично, доказывается, что если корень данного уравнения, то и корень этого уравнения.
Таким образом, мы доказали, что если корень уравнения
, то и корень данного уравнения и наоборот. Аналогично доказывается этот факт и для уравнения:
.
А значит, данные кубические многочлены имеют еще один общий иррациональный корень.
Для того, чтобы назвать модель математической, необходимо наличие трех вещей:
1) Ввести переменные
2) задать область, на которой будет рассмотрена задача
3) составить функцию цели. т.е. определить, как решать поставленную условием задачу.
Переменные берем из вопроса. Что надо найти? скорость каждого автомобиля. Поэтому введем переменные v₁ и v₂ - скорости первого и второго автомобилей соответственно.
Обе переменные больше нуля.
Расстояние можно найти, если знаем время и скорость. кратко запишем условие с таблицы.
s v t
1 автомобиль 180км ?v₁ 1ч.36мн=1 .6ч/после встречи/
2 автомобиль 180км ?v₂ 2ч 30 мин.=2.5ч/после встречи/
Расстояние Время
До встречи После встречи скорость до после
1 х 180-х v₁ одинак. 1.6
2 180-х х v₂ одинак. 2.5
Пусть первый до встречи проехал х км, тогда второй (180-х) км.
До встречи затратили одно и то же время, т.к. вышли одновременно.
х/v₁=(180-х)/ v₂
v₁1.6+ v₂*2.5=180
Составлена система двух уравнений с двумя переменными. Собственно цель - найти переменные - значения скоростей. После решения системы выполнить отбор полученных решений и записать ответ.
Поскольку, любое уравнение можно поделить на его старший коэффициент, то будем считать, для удобства, что мы рассматриваем два приведенных кубических уравнения с рациональными коэффициентами.
Поскольку, данные уравнения имеют общий корень, то уравнение, являющееся их разностью, тоже содержит этот корень:
А значит, данный общий иррациональный корень принимает вид :
, где 
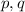- рациональные числа, при этом 
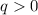не полный квадрат, отсюда в частности 
.
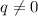Попробуем показать, что если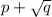
корень уравнения
Если число
является корнем данного уравнения , то сделаем замену: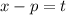 
, тогда после раскрытия скобок данное уравнение так же будет с рациональными коэффициентами и будет иметь корень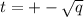 
Такое уравнение примет вид :
Учитывая, что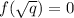
Предположим, что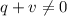
, но тогда , учитывая, что 
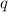- не полный квадрат, то левая часть равенства иррациональна, а правая рациональна, что невозможно. То есть мы пришли к противоречию, а значит :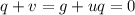 
Таким образом:
Аналогично, доказывается, что если![-\sqrt[]{q}](/tpl/images/1361/5367/ad7ea.png)
корень данного уравнения, то и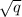 
корень этого уравнения.
Таким образом, мы доказали, что если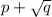
корень уравнения
А значит, данные кубические многочлены имеют еще один общий иррациональный корень.
Что и требовалось доказать.