Можно ли по последней цифре или по последним двум цифрам записи числа:
1) 288;
5) 12 569;
2) 3882;
6) 44 410;
3) 47 983;
7) 5625;
4) 677 547;
8) 3115
установить, что арифметический квадратный корень и
этого числа не является натуральным числом?

Показать ответ

Ответ:

Саня1585

11.06.2021 23:09

Відповідь:

1) 2ху – 3ху^2 = xy(2-3y)

2) 3х(х + 2) - 2(х + 2) = (x+2)(3x-2)

3) ав + 2ас + 2в + 4с = ав + 2в + 2ас + 4с = b(a+2) +2c(a+2) = (a+2)(b+2c)

4) 16а^2 – 9 = 4a^2-3^2 = (4a-3)(4a+3)

5) 3х^3 – 75х = 3х(x^2-25) = 3x(x-5)(x+5)

6) 2х^2 + 4ху + 2у^2 = 2(х^2 + 2ху + у^2) = 2(x+y)(x+y)

7) -2с^2 – 12сb – 18b^2 = -2(с^2 +6сb + 9b^2) = -2(c+2b)(c+2b)

8) с^3 – 16с = c(c^2-16) = c(c-4)(c+4)

9) -3у^2 + 6уb – 3b^2 = -3(у^2 - 2уb + b^2) = -3(y-b)(y-b)

10) 9х^2 – (х - 1)^2 = (3х)^2 – (х - 1)^2 = (3x - x +1)(3x + x -1) = (2x+1)(4x - 1)

11) х^3 + у^6 = х^3 + у^2^3 = (x+y^2)(x^2-xy^2+y^4)

12) 81а^4 – 1 = (9а^2)^2 - 1^2 = (9а^2 - 1)(9а^2 +1) = (3a-1)(3a+1)(9a^2+1)

13) 100а^4 – х^4 = (10а^2)^2 – (х^2)^2 = (10а^2 – х^2)(10а^2 + х^2) =

=(10а – х)(10а + х)(10а^2 + х^2)

14) x^2 – 3^х – 6^х + 9 = x(x-3) -3(x-3) = (x-3)(x-3) = (x-3)^2 // кажется ошибка в условии

Пояснення:

х^2 - х в степені 2

0,0(0 оценок)

Ответ:

Любознайка09

08.03.2020 16:03

1. Разложим, выделив полные квадраты где возможно и посмотрим, можно ли

$1) \ 4x^2-4xy+2y^2-2y+1=(2x)^2-2\cdot 2x\cdot y+y^2+y^2-2y+1 = \\ =(2x-y)^2+(y-1)^2$

Вот и получили сумму квадратов, а квадрат любого действительного числа (именно такие мы рассматриваем) неотрицателен, то данное выражение отрицательные значения принимать не может. ответ: нет.

$2) \ 1-8ab+4a^2b^2+4a^2+b^2 = (2a)^2-2\cdot 2a\cdot b+b^2 -4ab+4a^2b^2+1 = \\=(2a+b)^2+(2ab)^2-2\cdot2ab\cdot1+1^2 = (2a+b)^2+(2ab-1)^2$

Здесь ситуация аналогичная и ответ: нет.

2. Решаем уравнения

$1)\ y^3-24y^2=216-9y;\ y^2(y-24)-9(24-y)=0; \\ (y-24)(y^2+9)=0 \Rightarrow y=24$

Вторая скобка содержит в себе квадрат и положительное слагаемое, она всегда положительна, так что нулю может быть равна только первая скобка, откуда искомый корень и нашли. ответ: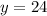 y=24

$2) \ 16x^3+12x^2=4x+3; \ 4x^2(4x+3)-(4x+3)=0; \\ (4x+3)(4x^2-1)=0; \ (4x+3)(2x-1)(2x+1)=0$

Произведение равно нулю, когда хотя бы один из сомножителей равен 0, это совокупность на языке множеств.

$\displaystyle (4x+3)(2x+1)(2x-1)=0 \Leftrightarrow \left[\begin{array}{ccc}4x+3=0\\2x+1=0\\2x-1=0\end{array} \Rightarrow \left[\begin{array}{ccc}x=-\frac{3}{4} \\x=-\frac{1}{2} \\x=\frac{1}{2} \end{array}$

В порядке убывания ответ будет такой:

$\displaystyle \frac{1}{2}; \ -\frac{1}{2}; \ -\frac{3}{4}$

3. Просто раскладываем:

$1) \4a^2-4b^2-a-b=4(a^2-b^2)-(a+b)=4(a-b)(a+b)-(a+b)= \\ =(a+b)(4(a-b)-1)=(a+b)(4a-4b-1) \\ 2) \ 9x^2-9y^2-3x+3y = 9(x^2-y^2)-3(x-y)=\\ =9(x-y)(x+y)-3(x-y)=3(x-y)(3(x+y)-1) = \\ =3(x-y)(3x+3y-1) \\ 3) 16p^2-y^2+8y-16 = (4p)^2 -(y^2-2\cdot y\cdot 4+4^2) = \\= (4p)^2-(y-4)^2 =(4p-(y-4))(4p+(y-4)) =\\ = (4p-y+4)(4p+y-4) \\ 4) \ 0.25a^2-a-b^2+1 = (0.5a)^2-2\cdot 0.5a\cdot1+1^2-b^2 = \\= (0.5a-1)^2-b^2 = (0.5a-1-b)(0.5a-1+b)$

4. Аналогично (если вы не проходили, корни, что вероятнее всего, так как это 7-ой класс, то в 1 примере последнее на пиши, остановись на предпоследнем шаге):

$1) \ a^3-7a^2-3a+21 = a^2(a-7)-3(a-7) = (a-7)(a^2-3) = \\ =(a-7)(a-\sqrt{3})(a+\sqrt{3}) \\ 2)\ 3x^4-8x^3+12x-32 = x^3(3x-8)+4(3x-8)=(3x-8)(x^3+4)\\ 3) \ a^5-6a^4+a^3-6a^2 = a^4(a-6)-a^2(a-6)=(a-6)(a^4-a^2) = \\ =(a-6)a^2(a^2-1)=a^2(a-6)(a-1)(a+1) \\ 4) \ 11x^7-11x^6+6x^5-6x^4 = 11x^6(x-1)+6x^4(x-1) =\\= (x-1)(11x^6+6x^4)=x^4(x-1)(11x^2+6)$

5. Тут уже даже первое действие дано

$1) \ 6b^2-6a^2-7b+7a=(6b^2-6a^2)-(7b-7a)=\\=6(b^2-a^2)-7(b+a) = 6(b-a)(b+a)-7(b+a)= \\ =(b+a)(6(b-a)-7)=(a+b)(6b-6a-7) \\ 2) x^4+x^3y-3x-3y = (x^4+x^3y)-(3x+3y) =\\= x^3(x+y)-3(x+y)=(x+y)(x^3-3)$