Перед тем как выражать , нужно рассмотреть случаи, когда дробь положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменной знак неравенства меняться не будет (так как делим (умножаем) на положительное число):
Решим неравенство методом интервалов.
а) ОДЗ:
б) Нуль неравенства:
в) Решением данного неравенства будет .
При таких значениях параметра знак неравенства меняться не будет:
Если такая дробь отрицательная, то при нахождении переменной знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):
Решим неравенство методом интервалов. Решением данного неравенства будет .
При таких значениях параметра знак неравенства изменится:
ответ: если , то ; если , то ; если и , то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если , то есть , то в объединении с получаем при Если , то есть , то в объединении с получаем, что таких не существует, то есть такого варианта эта система не имеет.
2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:
ответ: если , то ; если , то ; если , то система не имеет решений.
1) Иррациональные - это числа, которые нельзя выразить дробью a/b с целыми числителем и знаменателем. 2) Десятичные приближения по недостатку и по избытку - это десятичные дроби, между которыми заключено иррациональное число. Возьмём, например, √3~1,732. Его приближением до сотых долей по недостатку будет 1,73, а по избытку 1,74. 3) Классическое доказательство. Если √2 рационально, то его можно выразить несократимой дробью √2=a/b. Возведем все в квадрат. 2=a^2/b^2. То есть 2b^2=a^2. Теперь рассуждаем. Слева чётное число, значит a тоже чётное. Но чётный квадрат всегда делится на 4. Значит, b^2 тоже чётный. Но тогда а и b оба четные и дробь a/b можно сократить. Но мы условились, что дробь несократима. Противоречие. Значит, число √2 нельзя выразить дробью, то есть оно иррациональное. 4) Действительные - это все числа, и рациональные и иррациональные. 5) Действительные числа можно представить в виде точек на координатной прямой, причём это все точки на прямой. 6) Натуральные N, целые Z, рациональные Q, действительные R. Круги Эйлера нарисовать не могу, но могу объяснить. Действительные - самый большой круг, рациональные внутри, целые внутри рац-ных, натуральные внутри целых.
1. Решим первое неравенство этой системы:
ответ: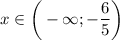
2. Дробь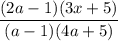 существует, если
существует, если
Перед тем как выражать , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 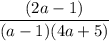 положительная, а когда отрицательная:
положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменнойРешим неравенство методом интервалов.
а) ОДЗ: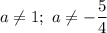
б) Нуль неравенства: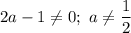
в) Решением данного неравенства будет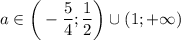 .
.
При таких значениях параметра знак неравенства меняться не будет:
знак неравенства меняться не будет:
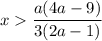
Если такая дробь отрицательная, то при нахождении переменнойРешим неравенство методом интервалов. Решением данного неравенства будет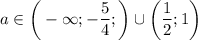 .
.
При таких значениях параметра знак неравенства изменится:
знак неравенства изменится:
ответ: если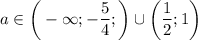 , то
, то 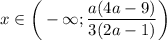 ; если
; если 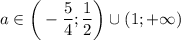 , то
, то 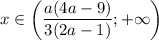 ; если
; если 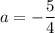 и
и 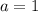 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:ответ: если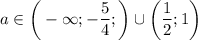 , то
, то 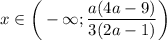 ; если
; если 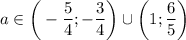 , то
, то 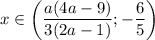 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.
2) Десятичные приближения по недостатку и по избытку - это десятичные дроби, между которыми заключено иррациональное число. Возьмём, например, √3~1,732. Его приближением до сотых долей по недостатку будет 1,73, а по избытку 1,74.
3) Классическое доказательство. Если √2 рационально, то его можно выразить несократимой дробью √2=a/b. Возведем все в квадрат. 2=a^2/b^2. То есть 2b^2=a^2. Теперь рассуждаем. Слева чётное число, значит a тоже чётное. Но чётный квадрат всегда делится на 4. Значит, b^2 тоже чётный. Но тогда а и b оба четные и дробь a/b можно сократить. Но мы условились, что дробь несократима. Противоречие. Значит, число √2 нельзя выразить дробью, то есть оно иррациональное.
4) Действительные - это все числа, и рациональные и иррациональные.
5) Действительные числа можно представить в виде точек на координатной прямой, причём это все точки на прямой.
6) Натуральные N, целые Z, рациональные Q, действительные R. Круги Эйлера нарисовать не могу, но могу объяснить. Действительные - самый большой круг, рациональные внутри, целые внутри рац-ных, натуральные внутри целых.