(2+√5) = 1/8 + 3√5/8 + 15/8 + 5√5/8 = (1/2 + √5/2)³ = (1 + √5)³/8
(2 - √5) = 1/8 - 3√5/8 +15/8 - 5√5/5 = (1/2 - √5/2)³ = (1 - √5)³/ 8
∛(2 + √5) + ∛(2 - √5) = ∛(1 + √5)³/2³ + ∛(1 - √5)³/2³ = (1 + √5)/2 + (1 - √5)/2 = 1/2 - √5/2 + 1/2 + √5/2 = 1
ответ ОДИН
сделаем по другому
a = 2 + √5
b = 2 - √5
∛(2 + √5) + ∛(2 -√5) = c
∛(a*b) = ∛((2 + √5)(2 - √5)) = ∛(-1) = -1 (формула 1)
a + b = 2 + √5 + 2 - √5 = 4 (формула 2)
∛a + ∛b = c
∛a = c - ∛b (возводим в куб) (формула 3)
a = c³ - 3c²∛b + 3c∛b² - b
c³ = a + 3c²∛b - 3c∛b² + b = a + b + 3c∛b(c - ∛b) ={ по формуле 2 и 3} = 4 + 3c∛b*∛a = {формула 1} =4 - 3c
c³ + 3c - 4 = 0
c³ + c² + 4c - c² - c - 4 = 0
c²(c - 1) + c(c -1) + 4(c-1) = 0
(c - 1)(c² + c + 4) = 0
вспоминаем что ∛(2 + √5) + ∛(2 -√5) = c
первая скобка c = 1
вторая скобка c² + c + 4 = 0 D=1 - 4*4 = -15 дискриминант отрицательный, действительных решений нет (2 комплексных)
ответ 1
Объяснение:
1. E
2. Д
4+21-8
3. Д
4. В
5. А
x(2x-7)=0 x=0 или x=3,5
6. В
D=9-4*2*(-5)=49
7. В
D=1-4*1*(-20)=81
x1=(-1+9)/2=4 x2=(-1-9)/2=5
8. А
4y²-12y+9=y²+4y+4
3y²-16y+5=0
D=14² y1=5 y2=1/3
9. С
D=81-4*5*(-2)=121
x1=(9+11)/10 x1=2 x2=(9-11)/10=-0,2
сумма корней: 2-0,2=1,8
10. нет корней , в записи уравнения ошибка видимо в знаке
11. Д
Приводим к общему знаменателю, при этом знаменатель не равен 0 и отбрасываем его, приравниваем числитель к 0:
5y²-15y-4y²+8y-y(y²-5y+6)=0
-y³+6y²-13y=0
y(y²-6y+13)=0 y≠0 по ОДЗ и второе уравнение не имеет корней
12. А
Пользуемся формулой ax²+bx+c=a(x-x1)(x-x2)
легко найти корни: x1=-5 и x2=1/3 подставляем:
3(x-(-5))(x-1/3)= заносим 3 во вторую скобку: (x+5)(3x-1)
(2+√5) = 1/8 + 3√5/8 + 15/8 + 5√5/8 = (1/2 + √5/2)³ = (1 + √5)³/8
(2 - √5) = 1/8 - 3√5/8 +15/8 - 5√5/5 = (1/2 - √5/2)³ = (1 - √5)³/ 8
∛(2 + √5) + ∛(2 - √5) = ∛(1 + √5)³/2³ + ∛(1 - √5)³/2³ = (1 + √5)/2 + (1 - √5)/2 = 1/2 - √5/2 + 1/2 + √5/2 = 1
ответ ОДИН
сделаем по другому
a = 2 + √5
b = 2 - √5
∛(2 + √5) + ∛(2 -√5) = c
∛(a*b) = ∛((2 + √5)(2 - √5)) = ∛(-1) = -1 (формула 1)
a + b = 2 + √5 + 2 - √5 = 4 (формула 2)
∛a + ∛b = c
∛a = c - ∛b (возводим в куб) (формула 3)
a = c³ - 3c²∛b + 3c∛b² - b
c³ = a + 3c²∛b - 3c∛b² + b = a + b + 3c∛b(c - ∛b) ={ по формуле 2 и 3} = 4 + 3c∛b*∛a = {формула 1} =4 - 3c
c³ + 3c - 4 = 0
c³ + c² + 4c - c² - c - 4 = 0
c²(c - 1) + c(c -1) + 4(c-1) = 0
(c - 1)(c² + c + 4) = 0
вспоминаем что ∛(2 + √5) + ∛(2 -√5) = c
первая скобка c = 1
вторая скобка c² + c + 4 = 0 D=1 - 4*4 = -15 дискриминант отрицательный, действительных решений нет (2 комплексных)
ответ 1
Объяснение:
1. E
2. Д
4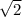 +21
+21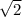 -8
-8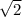
3. Д
4. В
5. А
x(2x-7)=0 x=0 или x=3,5
6. В
D=9-4*2*(-5)=49
7. В
D=1-4*1*(-20)=81
x1=(-1+9)/2=4 x2=(-1-9)/2=5
8. А
4y²-12y+9=y²+4y+4
3y²-16y+5=0
D=14² y1=5 y2=1/3
9. С
D=81-4*5*(-2)=121
x1=(9+11)/10 x1=2 x2=(9-11)/10=-0,2
сумма корней: 2-0,2=1,8
10. нет корней , в записи уравнения ошибка видимо в знаке
11. Д
Приводим к общему знаменателю, при этом знаменатель не равен 0 и отбрасываем его, приравниваем числитель к 0:
5y²-15y-4y²+8y-y(y²-5y+6)=0
-y³+6y²-13y=0
y(y²-6y+13)=0 y≠0 по ОДЗ и второе уравнение не имеет корней
12. А
Пользуемся формулой ax²+bx+c=a(x-x1)(x-x2)
легко найти корни: x1=-5 и x2=1/3 подставляем:
3(x-(-5))(x-1/3)= заносим 3 во вторую скобку: (x+5)(3x-1)