на координат ной прямой отмечены числа a, b и c. отметьте на этой прямой какое нибудь число x так, чтобы при этом выполнялись три условия :-a+x>0,-x+b>0,x-c<0
Поскольку график данной функции проходит через точку М(3; -1/11), то имеем: -1/11 = 1/(-9 + 3а - 4); -1/11 = 1/(-13 + 3а); -13 + 3а = -11; 3а = 2; а = 2/3.
у = 1/(-х² + (2/3)х - 4)
Наименьшее значение этой функции совпадает с наибольшим значением функции f(x) = -х² + (2/3)х - 4 (наибольшим значением знаменателя), которое равно значению ординаты вершины прараболы f(x) = -х² + (2/3)х - 4.
Поскольку график данной функции проходит через точку М(3; -1/11), то имеем: -1/11 = 1/(-9 + 3а - 4); -1/11 = 1/(-13 + 3а); -13 + 3а = -11; 3а = 2; а = 2/3.
у = 1/(-х² + (2/3)х - 4)
Наименьшее значение этой функции совпадает с наибольшим значением функции f(x) = -х² + (2/3)х - 4 (наибольшим значением знаменателя), которое равно значению ординаты вершины прараболы f(x) = -х² + (2/3)х - 4.
х₀ = -b/(2a) = -(2/3)/(-2) = 1/3 - абсциса вершины, f(1/3) = -1/9 + 2/9 - 4 = -35/9 - ордината вершины.
Значит y = 1/(-35/9) = -9/35 - наименьшее значение данной функции.
ответ: -9/35.
угол между прямой и плоскостью, это угол между прямой и ее проекцией на эту плоскость.
точка C1 проецируется в точку C => отрезок AC1 проецируется в диагональ AC.
угол CAC1=60°
Из треугольника ACC1:
CO=BO из свойств прямоугольника => треугольник COB равнобедренный.
2∠OBC+∠COB=180° (как углы треугольника)
∠OBC=(180-30)/2=75°
Из треугольника DCB, ∠CDB=180°-90°-75°=15°
AC=BD из свойств прямоугольника.
Раскрывать синус и косинус 15 глупо, но это легко можно сделать например как sin(45-30) или sin(60-45) или sin(30/2).
------------------
ответ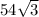
Если что-то непонятно задай вопрос