На переезде у семафора автомобиль был задержан на 6мин. Чтобы прибыть в пункт назначения вовремя, он увеличил скорость на 10км/ч.
Найдите скорость автомобиля после переезда, если расстояние между переездом и пунктом назначения равно 42 км.
Нужно полное объяснение задачи

Итак, окончательно мы решили, что n и m - целые числа. Проделаем 2018 операций следующего вида: возводим равенство в квадрат и переносим n вправо. Получаем равенство

Справа стоит целое число, n является его квадратом. Для нас важно только, что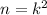 для некоторого целого неотрицательного числа.  Перенося n налево и заменяя 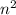на k, получаем равенство вида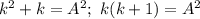

1-й случай. k=0; n=0; m=0. Автор задачи про этот случай знает.

2-й случай. k>0. Докажем, что произведение двух соседних натуральных чисел не может быть полным квадратом. k=1; k+1=2, произведение равно 2 - это не есть полный квадрат. k=2; k+1=3; произведение равно 6 - это не есть полный квадрат. Почему ни при каком натуральном k произведение не может быть полным квадратом? Дело в том, что у соседних натуральных чисел не может быть общих множителей, кроме 1. Поэтому, если их произведение является полным квадратом, каждое из этих чисел должно быть полным квадратом, чего быть не может быть - единственный случай, когда расстояние между квадратами целых неотрицательных чисел равно 1 - это 0 и 1, а этот случай мы уже рассмотрели.

ответ: n=m=0

а) z* = -z·i

z = x + iy

x - iy = -(x + iy)·i

x - iy = -ix + y

x + ix = y + iy

x·(1 + i) = y·(1 + i)

y = x

z = x + ix, x ∈ R

б) 2·|z| - 8z + 1 + 2i = 0

z = x + iy

2√(x² + y²) - 8·(x + iy) + 1 + 2i = 0

2√(x² + y²) - 8x - i8y + 1 + 2i = 0

2√(x² + y²) = (8x - 1) + i(8y - 2)

2√(x² + y²) = 8x - 1

8y - 2 = 0

y = 1/4

2√(x² + (1/4)²) = 8x - 1

4(x² + 1/16) = 64x² - 16x + 1

8x - 1 ≥ 1/2

4x² + 1/4 = 64x² - 16x + 1

8x ≥ 3/2

60x² - 16x + 3/4 = 0

x ≥ 3/16

240x² - 64x + 3 = 0

D = 64² - 4·240·3 = 1216

x = (64 (+/-) √1216)/480 = (64 (+/-) 8√19)/480 = (8 (+/-) √19)/60

x = 2/15 (+/-) √19/60

x ≥ 3/16

x = 2/15 + √19/60

z = 2/15 + √19/60 + i/4