На первой автостоянке стояло в 8 раз автомобилей больше, чем на второй. Когда с первой автостоянки на вторую перевезли 25 автомобилей, то на второй стоянке оказалось в 2 раза больше машин, чем на первой. Сколько автомобилей было на каждой стоянке первоначально
(12/x)+1=(12/y), т.е. первому потребовалось на один час больше чтобы дойти до середины чем другому.
24/(x+y)=2,4, т.е. им вдвоем нужно 2,4 часа, чтобы км.
Решим систему уравнений, преобразуя сперва второе уравнение:
24/(x+y)=2, домножим на (x+y)
24=2,4x+2.4y
10=x+y
x=10-y
Подставим значение x в первое уравнение:
12/(10-y)+1=12/y. Умножим обе части на (10-y)*(y)
12y+10y-y^2=120-12y
-y^2+34y-120=0
D=676
y1=(-34+26)/-2=4
y2=(-34-26)/-2=30
x=10-y
x1=10-4=6
x2=10-30=-20, посторонний корень, так как x должен быть >0.
Значит, скорость одного 4км/ч, скорость другого 6км\ч.
1. Используя формулу n-го члена арифметической прогрессии: an = a1 + (n-1)d, решим следующую систему уравнений
***************************************************************************************************
2.
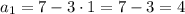
Имеем арифметическую прогрессию с первым членом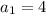
и разностью прогрессии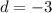 
Сумма первых 12 членов арифметической прогрессии, равна:
**************************************************************************************************
3. Разность прогрессии: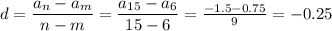
Первый член арифметической прогрессии: