Или , где (m ; n) - координаты вершины параболы.
На рисунке видно, что координаты вершины параболы (2 ; 2) .
Координаты любой точки параболы, например (0 ; - 2) .
Подставим эти значения в формулу и найдём а :
-62
Объяснение:
f(x)=ax²+bx+c
Определим коэффициенты a, b, с.
1) Коэффициент а находим по формуле y=a(x-m)²+n, где (m;n) - координаты вершины параболы, а (х;у) - координата любой точки параболы, например, (1;1).
m=2; n=2
a(1-2)²+2=1
a(-1)²=-1
a*1=-1
a=-1
2) Коэффициент b находим из формулы для вершины параболы:
-b/2a = m
b = -m*2a =-2*2*(-1)=4
3) Коэффициент с найдём как ординату пересечения параболы с осью Оу. Искомая точка (0;-2), значит, с=-2
4) Запишем уравнение параболы: f(x) = -x²+4x-2
5) Находим f(10):
f(10)= -10²+4*10-2 = -100+40-2 = -62
Или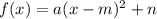 , где (m ; n) - координаты вершины параболы.
, где (m ; n) - координаты вершины параболы.
На рисунке видно, что координаты вершины параболы (2 ; 2) .
Координаты любой точки параболы, например (0 ; - 2) .
Подставим эти значения в формулу и найдём а :
-62
Объяснение:
f(x)=ax²+bx+c
Определим коэффициенты a, b, с.
1) Коэффициент а находим по формуле y=a(x-m)²+n, где (m;n) - координаты вершины параболы, а (х;у) - координата любой точки параболы, например, (1;1).
m=2; n=2
a(1-2)²+2=1
a(-1)²=-1
a*1=-1
a=-1
2) Коэффициент b находим из формулы для вершины параболы:
-b/2a = m
b = -m*2a =-2*2*(-1)=4
3) Коэффициент с найдём как ординату пересечения параболы с осью Оу. Искомая точка (0;-2), значит, с=-2
4) Запишем уравнение параболы: f(x) = -x²+4x-2
5) Находим f(10):
f(10)= -10²+4*10-2 = -100+40-2 = -62