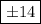Начерти окружности с данными центрами O и B и данными радиусами: r1 = 14,3 см, r2 = 7,1 см — так, чтобы они имели одну общую точку.

Показать ответ

Ответ:

Andreyzem4

18.12.2022 10:51

Объяснение:

Для того, чтобы вычислить площадь фигуры, ограниченной данными линиями, мы сперва должны построить их на графике

Теперь мы видим, что функцией y = 0, наша искомая фигура разбивается на две симметричные. Их площадь будет равна, то есть для того, чтобы вычислить площадь фигуры, нам достаточно найти площадь одной её половины и умножить на "2".

Получается, площадь равна удвоенному интегралу функции х^3 от 2 до 0.

2 * инт (х^3)dx = 2 * (x^4)/4.

Подставляем наши границы "2" и "0": 2 * (x^4)/4 = 2 * ((2^4)/4 - (0^4)/4) = 2 * 4 = 8.

ответ: S фигуры = 8.

0,0(0 оценок)

Ответ:

xato2003

06.11.2021 08:09

$$9x^2+\frac{25}{x^2}=226;$

Попробуем в левой части выделить полный квадрат, как раз от выражения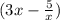 $(3x-\frac{5}{x})$

$$(3x)^2-2\cdot 3x\cdot \frac{5}{x} + (\frac{5}{x})^2+2\cdot 3x\cdot \frac{5}{x}=226;$

Здесь удвоенное произведение я искусственно создал для выделения квадрата, но чтобы не нарушить равенства, надо это же удвоенное произведение с противоположным знаком добавить, что и было сделано.

$$(3x-\frac{5}{x})^2+ 30=226; (3x-\frac{5}{x})^2=196=(\pm14)^2 \Rightarrow$

$$(3x-\frac{5}{x})=\pm 14$

Было получено два значения и не зря. Если решать уравнение из условия, то мы обязательно получим 2 корня (кроме случая x=0, на котором даже не определено второе слагаемое и потому его в расчет не берем), это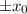 $\pm x_0$ и второе выражение, которое зависит от этих корней, может и будет принимать не одно лишь значение, а 2.