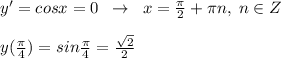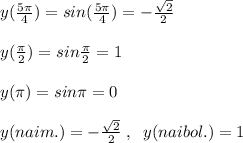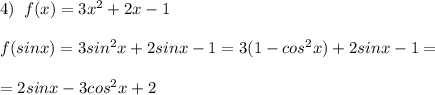Надо! ! 1)найдите наименьшее и наибольшее значение функции y=sinx на отрезке [p/6; 7p/6] 2)известно, что f(x)=2x^2+3x-2. докажите, что f(sinx)= 3sinx-2cos^2x 3)найдите наименьшее и наибольшее значение функции y=sinx на отрезке [p/4; 5p/4] 4)известно, чтоf(x)=3x^2+2x-1 докажите, что f(sinx)=2sinx-3cos^2x+2
![1)\quad y=sinx\; ,\; \; x\in [ \frac{\pi}{6} ; \frac{7\pi}{6} ]\\\\y'=cosx=0\; \; \to \; \; x=\frac{\pi}{2}+\pi n,\; n\in Z\\\\y(\frac{\pi}{2})=sin\frac{\pi }{2}=1\\\\y(\pi )=sin\pi =0\\\\y(\frac{\pi}{6})=\frac{1}{2}\\\\y(\frac{7\pi}{6})=-\frac{1}{2}\\\\y(naimen.)=-\frac{1}{2}\; ,\; \; y(naibol.)=1](/tpl/images/0662/2443/c87b4.png)
![2)\; \; f(x)=2x^2+3x-2\\\\f(sinx)=2sin^2x+3sinx-2=2(1-cos^2x)+3sinx-2=\\\\=3sinx-2cos^2x\\\\3)\; \; y=sinx\; \; ,\; \; x\in [ \frac{\pi}{4} ; \frac{5\pi }{4} ]](/tpl/images/0662/2443/70907.png)