Пусть скорость туриста на подъёме равна x км/ч, тогда его скорость на спуске равна ( x + 0,6 ) км/ч. Если спуск занял 1,5 часа, то пройденное за это время расстояние составит ( x + 0,6 ) * 1,5 = 1,5x + 0,9 км.
Если весь путь занял 2 часа, а спуск - 1,5 часа, то подъём занял 2 - 1,5 = 0,5 часа. За это время турист (двигаясь со скоростью x км/ч) 0,5 * x = 0,5x км.
Учитывая, что весь путь равен 7,2 км, можно составить уравнение:
Скорость на подъёме составила 3,15 км/ч, следовательно скорость на спуске равна 3,15 + 0,6 = 3,75 км/ч.
Теперь если поделить V₂ на V₁ (V₁ = × π × r² × h), то получим 0.847, в столько раз второй объем меньше чем первый, или же это можно записать как 100% - 84,7% = 15,3 %
3,75 км/ч.
Объяснение:
Пусть скорость туриста на подъёме равна x км/ч, тогда его скорость на спуске равна ( x + 0,6 ) км/ч. Если спуск занял 1,5 часа, то пройденное за это время расстояние составит ( x + 0,6 ) * 1,5 = 1,5x + 0,9 км.
Если весь путь занял 2 часа, а спуск - 1,5 часа, то подъём занял 2 - 1,5 = 0,5 часа. За это время турист (двигаясь со скоростью x км/ч) 0,5 * x = 0,5x км.
Учитывая, что весь путь равен 7,2 км, можно составить уравнение:
Скорость на подъёме составила 3,15 км/ч, следовательно скорость на спуске равна 3,15 + 0,6 = 3,75 км/ч.
Второй объем меньше первого на 15,3 %
Объяснение:
Изначально радиус конуса r был 100%. Теперь же его увеличили на 10%, и теперь радиус конуса r₂ равен 110%. Так же это можно записать как:
r₂ = 1,1 × r
Теперь к высоте. С ней все тоже самое, только уменьшили. Значит h = 100%, a h₂ = 70%. То есть h₂ = 0,7 × h
Подставляем новые данные в формулу:
V₂ =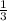
× π × (1,1 × r)² × 0,7 × h = 
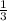× π × 1,21r² × 0,7h
Теперь если поделить V₂ на V₁ (V₁ =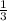
× π × r² × h), то получим 0.847, в столько раз второй объем меньше чем первый, или же это можно записать как 100% - 84,7% = 15,3 %