Касательная - прямая, которая касается к кривой в точке (x₀;3), где x₀ - абсцисса касания. Подставим координаты точки касания в заданное уравнение кривой
Путем подбора , уравнение имеет единственный корень, так как функция, соответствующая данному уравнению, является монотонной.
(-1;3) - точка касания касательной.
Найдем теперь значение производной в точке (-1;3).
Касательная - прямая, которая касается к кривой в точке (x₀;3), где x₀ - абсцисса касания. Подставим координаты точки касания в заданное уравнение кривой
Путем подбора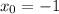 , уравнение имеет единственный корень, так как функция, соответствующая данному уравнению, является монотонной.
, уравнение имеет единственный корень, так как функция, соответствующая данному уравнению, является монотонной.
(-1;3) - точка касания касательной.
Найдем теперь значение производной в точке (-1;3).
Уравнение касательной к кривой:
Уравнение нормали к кривой: