Написати контрольну роботу з алгебри.
1. Знайдіть різницю арифметичної прогресії 8; 9,5; 11; 12,5...
2. Дано геометричну прогресію (вn). Знайдіть третій член, якщо перший член дорівнює 4, а знаменник дорівнює -1/2.
3. Знайдіть суму нескінченної геометричної прогресії, перший член якої дорівнює -12, а q=1/2.
4. Знайдіть номер члена арифметичної прогресії, який дорівнює 10,9, а перший член дорівнює 8,5, а різниця дорівнює 0,3.
5. Між числами 2,5 і 20 вставте два таких числа, щоб вони разом з даними утворювали геометричну прогресію.
6. Обчисліть перший член та різницю арифметичної прогресії(an), якщо a2+ a15=32; a6+a17=44.
7. Знайдіть суму всіх натуральних чисел, більших за 100 і менших від 200, які кратні 6.
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)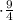
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: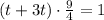
9t = 1
Значит,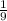
- цис./ч - производительность "медленного" насоса.
Тогда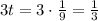
- цис./ч - производительность "быстрого" насоса.
Следовательно,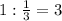
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
1) 2sin x-1=0
sinx = 1/2
x = (-1)^n arcsin(1/2) + πk, k∈Z
x = (-1)^n (π/6) + πk, k∈Z
2) cos(2x+П/6)+1=0
cos(2x+П/6) = - 1
2x+П/6 = π + 2πn, n∈Z
2x = π - π/6 + 2πn, n∈Z
2x = 5π/6 + 2πn, n∈Z
x = 5π/12 + πn, n∈Z
3) 6sin²x - 5cosx + 5 = 0
6(1 - cos²x) - 5cosx + 5 = 0
6 - 6cos²x - 5cosx + 5 = 0
6cos²x + 5cosx - 11 = 0
cosx = t, ItI ≤ 1
6t² + 5t - 11 = 0
D = 25 + 4*6*11 = 289
t₁ = (- 5 - 17)/12
t₁ = - 22/12
t₁ = -11/6
t₁ = - 1 (5/6) не удовлетворяет условию ItI ≤ 1
t₂ = (- 5 + 11)/12
t₂ = 1/2
cosx = 1/2
x = (+ -)arccos(1/2) + 2πm, m∈Z
x = (+ -) *(π/3) + 2πm, m∈Z