Алгебра: напишите дано,решение,найти

напишите дано,решение,найти

Показать ответ

Ответ:

belover

27.06.2022 11:18

Решение:

Рисунок смотрите в приложении (на нем изображены равные векторы).

Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).

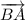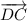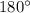а). Векторы $\overrightarrow{BA}$ и $\overrightarrow{DC}$ равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен $180 ^\circ$ градусов (получаем, что это коллинеарные, но не равные векторы).

$\overrightarrow{BA} \neq \overrightarrow{DC}$ .

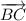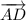б). Векторы $\overrightarrow{BC}$ и $\overrightarrow{AD}$ равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.

$\overrightarrow{BC} = \overrightarrow{AD}$ .

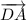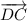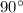в). Векторы $\overrightarrow{DA}$ и $\overrightarrow{DC}$ опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - $90^\circ$ градусов).

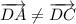
$\overrightarrow{DA} \neq \overrightarrow{DC}$

ответ:

а) нет;

б) да;

в) нет.

Abcd – квадрат. равны ли векторы: а) ва и dc; б) вс и ad; в) da и dc?

0,0(0 оценок)

Ответ:

Karina11222

20.12.2020 18:04

ответ: 3,75 км/ч, 5,25 км/ч.

Пусть х км/ч скорость первого пешехода, а у км/ч – скорость второго пешехода.

Тогда за 3 ч 20 минут (3ч 20 мин = 3ч + 20/60 ч = 3 1/3 ч = 10/3 ч) первый пешеход х/3 км, второй пешеход у/3 км. Общее пройденное расстояние равно 30 км:

10х/3 + 10у/3 = 30.

Если бы первый пешеход вышел на 2 ч раньше, то до встречи он бы шел 2 + 2,5 = 4,5 часа и бы 4,5х км. А второй пешеход двигался бы 2,5 часа и у км.

4,5х + 2,5у = 30.

Составим систему уравнений:

10х/3 + 10у/3 = 30,

4,5х + 2,5у = 30.

умножим обе части первого уравнения на 3, обе части второго на 2:

10х + 10у = 90,

9х + 5у = 60.

Умножим обе части второго уравнения на 2:

10х + 10у = 90,

18х + 10у = 120.