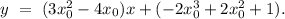Не дана координата точки касания. Напишем общий вид уравнения касательной для произвольной точки х0.
Производная:
Тогда уравнение касательной будет иметь вид:
ответ:
Не дана координата точки касания. Напишем общий вид уравнения касательной для произвольной точки х0.
Производная:
Тогда уравнение касательной будет иметь вид:
ответ: