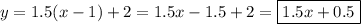Общий вид уравнения касательной:
1) Вычислим значение функции в точке x₀ = 1, получим:
Теперь найдем производную функции:
2) Вычислим значение производной в точке x₀ = 1, получим
Уравнение касательной:
Общий вид уравнения касательной: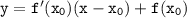
1) Вычислим значение функции в точке x₀ = 1, получим:
Теперь найдем производную функции:
2) Вычислим значение производной в точке x₀ = 1, получим
Уравнение касательной: