Неопределённость оо/оо. Чтобы раскрыть такую неопределённость обычно числитель и знаменатель делят на эн в максимальной степени. Для этого достаточно раскрыть скобки, привести подобные, найти эн в максимальной степени и разделить числитель и знаменатель на него. Что мы и проделаем, но попутно будем делать упрощения, если получится. Для удобства сначала числитель преобразуем, потом знаменатель.
Числитель раскладываем по формуле разности квадратов. Причём два раза.
Знаменатель раскладываем по формуле суммы кубов
Находим отношение числителя к знаменателю
Вот теперь переходим непосредственно к нахождению предела. Находим, что максимальная степень эн - это квадрат. Вот на эн в квадрате () и будем делить числитель и знаменатель
При подстановке бесконечности получаем деление константы на бесконечность, что равно нулю.
Первые два в промежуток не попадают, третий - попадает.
при имеем корни
,
первый корень в промежуток не попадает, другие два - попадают.
Если подставлять , то увидим, что полученные в итоге корни уже не будут вписываться в границы отрезка.
универсальный, но не очень удобный): оценить и проверить, при каких целых неравенство имеет решение. Для этого все серии корней по отдельности подставляем вместо :
Очевидно, что целых , удовлетворяющих последнему неравенству, не существует. Т.е. ни один из корней этой серии промежутку не принадлежит.
Последнему неравенству удовлетворяет только одно целое - . Корень находим при подстановке значения в соответствующую серию.
То же можно проделать с третьей серией и убедиться, что неравенство удовлетворяют только 2 значения и . Их также подставляем в соответствующую серию и находим корни.
Неопределённость оо/оо. Чтобы раскрыть такую неопределённость обычно числитель и знаменатель делят на эн в максимальной степени. Для этого достаточно раскрыть скобки, привести подобные, найти эн в максимальной степени и разделить числитель и знаменатель на него.
Что мы и проделаем, но попутно будем делать упрощения, если получится. Для удобства сначала числитель преобразуем, потом знаменатель.
Числитель раскладываем по формуле разности квадратов. Причём два раза.
Знаменатель раскладываем по формуле суммы кубов
Находим отношение числителя к знаменателю
Вот теперь переходим непосредственно к нахождению предела. Находим, что максимальная степень эн - это квадрат. Вот на эн в квадрате (
При подстановке бесконечности получаем деление константы на бесконечность, что равно нулю.
просто подряд подставлять целые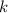
при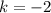 имеем корни
имеем корни
Первые два в промежуток не попадают, третий - попадает.
при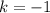 имеем корни
имеем корни
первый корень в промежуток не попадает, другие два - попадают.
Если подставлять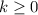 , то увидим, что полученные в итоге корни уже не будут вписываться в границы отрезка.
, то увидим, что полученные в итоге корни уже не будут вписываться в границы отрезка.
универсальный, но не очень удобный): оценить и проверить, при каких целых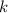 неравенство
неравенство 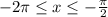 имеет решение. Для этого все серии корней по отдельности подставляем вместо
имеет решение. Для этого все серии корней по отдельности подставляем вместо  :
:
Очевидно, что целых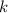 , удовлетворяющих последнему неравенству, не существует. Т.е. ни один из корней этой серии промежутку не принадлежит.
, удовлетворяющих последнему неравенству, не существует. Т.е. ни один из корней этой серии промежутку не принадлежит.
Последнему неравенству удовлетворяет только одно целое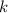 -
- 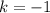 . Корень находим при подстановке значения
. Корень находим при подстановке значения 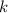 в соответствующую серию.
в соответствующую серию.
То же можно проделать с третьей серией и убедиться, что неравенство удовлетворяют только 2 значения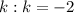 и
и 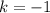 . Их также подставляем в соответствующую серию и находим корни.
. Их также подставляем в соответствующую серию и находим корни.