1) 899 = 31*29; 1364 = 4*11*31; НОД = 31 2) Одно число х, второе 1,5х (x + 1,5x)/2 = 2,34 2,5x = 4,68 x = 1,872 - это меньшее число 1,5x = 2,808 - это большее число 3) Скорость сближения равна 60 + 90 = 150 км/ч = 150000/3600 м/с = 125/3 м/с За 15 с он проехал 125*5 = 625 м. Это и есть длина поезда. 4) Карандаш стоит x руб, а ручка 1,3x руб. С другой стороны, альбом стоит y руб, а ручка 0,78y руб. Но цена ручки одна и та же. 1,3x = 0,78y x = y*0,78/1,3 = y*6/10 = 0,6y Карандаш дешевле альбома на 40% 5) 8! = 40320
кубическая функция может иметь только локальный минимум. Потому что при х -> она уходит в
точки минимума и максимума соответствуют нулям производной
сумма степеней равна нулю, значит один корень = 1, второй = a
локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)
значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7
2) Одно число х, второе 1,5х
(x + 1,5x)/2 = 2,34
2,5x = 4,68
x = 1,872 - это меньшее число
1,5x = 2,808 - это большее число
3) Скорость сближения равна
60 + 90 = 150 км/ч = 150000/3600 м/с = 125/3 м/с
За 15 с он проехал 125*5 = 625 м. Это и есть длина поезда.
4) Карандаш стоит x руб, а ручка 1,3x руб.
С другой стороны, альбом стоит y руб, а ручка 0,78y руб.
Но цена ручки одна и та же.
1,3x = 0,78y
x = y*0,78/1,3 = y*6/10 = 0,6y
Карандаш дешевле альбома на 40%
5) 8! = 40320
кубическая функция может иметь только локальный минимум. Потому что при х ->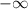
она уходит в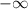 
точки минимума и максимума соответствуют нулям производной
сумма степеней равна нулю, значит один корень = 1, второй = a
локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)
значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7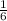
при а>1 локальный минимум f(x=a) = a^3/3-(a+1)/2*a^2+a^2 - 7 = (1/3 - 1/2) a^3 + (-1/2+1) a^2 - 7 = - a^3 / 6 + a^2 / 2 - 7
при a = 1 имеем точку перегиба и никакого минимума