Заметим, что сумма цифр у числа будет иметь такой же остаток по модулю 9, что и само число, так как пусть число имеет вид заметим, что число вида 10^n-1 делится на 9, так как оно будет состоять из одних девяток, значит число вида сравнимо с по модулю 9. Значит все число сравнимо с суммой цифрой по модулю 9. Так как 209! делится на 9 (содержит множитель 9), то сумма цифр будет делится на 9 ⇒ сумма суммы цифр делится на 9 и. т.д. Таким образом, однозначное число будет делится на 9, значит оно равно 0 или 9, но равно 0 оно быть не может, так как сумма цифр у натурального числа ненулевая, так как содержит хотя бы 1 не 0. Значит она равна 9
Объяснение:
2) x²+y²=74
x-y=2; y=x-2
x²+(x-2)²=74
x²+x²-4x+4=74
2x²-4x+4-74=0
2x²-4x-70=0
x²-2x-35=0; D=4+140=144
x₁=(2-12)/2=-10/2=-5; y₁=-5-2=-7
x₂=(2+12)/2=14/2=7; y₂=7-2=5
ответ: (-5; -7) и (7; 5).
3) x²+4y²=34
x+y=7; y=7-x
x²+4(7-x)²=34
x²+4(49-14x+x²)=34
x²+196-56x+4x²-34=0
5x²-56x+162=0; D=3136-3240=-104
При D<0 данная система не имеет решений.
4) x²-2xy-y²=1
x+y=2; y=2-x
x²-2x(2-x)-(2-x)²=1
x²-4x+2x²-4+4x-x²-1=0
2x²-5=0; D=40
x₁=-(2√10)/4=-(√10)/2; y₁=2 +(√10)/2=(4+√10)/2
x₂=(2√10)/4=(√10)/2; y₂=2 -(√10)/2=(4-√10)/2
ответ: (-(√10)/2; (4+√10)/2) и ((√10)/2; (4-√10)/2).
9
Объяснение:
Заметим, что сумма цифр у числа будет иметь такой же остаток по модулю 9, что и само число, так как пусть число имеет вид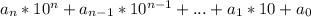 заметим, что число вида 10^n-1 делится на 9, так как оно будет состоять из одних девяток, значит число вида
заметим, что число вида 10^n-1 делится на 9, так как оно будет состоять из одних девяток, значит число вида 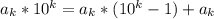 сравнимо с
сравнимо с 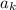 по модулю 9. Значит все число сравнимо с суммой цифрой по модулю 9. Так как 209! делится на 9 (содержит множитель 9), то сумма цифр будет делится на 9 ⇒ сумма суммы цифр делится на 9 и. т.д. Таким образом, однозначное число будет делится на 9, значит оно равно 0 или 9, но равно 0 оно быть не может, так как сумма цифр у натурального числа ненулевая, так как содержит хотя бы 1 не 0. Значит она равна 9
по модулю 9. Значит все число сравнимо с суммой цифрой по модулю 9. Так как 209! делится на 9 (содержит множитель 9), то сумма цифр будет делится на 9 ⇒ сумма суммы цифр делится на 9 и. т.д. Таким образом, однозначное число будет делится на 9, значит оно равно 0 или 9, но равно 0 оно быть не может, так как сумма цифр у натурального числа ненулевая, так как содержит хотя бы 1 не 0. Значит она равна 9