Пускай скорость пассажирского поезда будет х км/ч. Тогда скорость товарного поезда будет х-20 км/ч. Время, за которое пассажирский поезд пройдёт 480 км, пусть будет у ч, тогда время товарного поезда будет у+4 ч. Имеем систему уравнений: х×у=480, (х-20)×(у+4)=480. х=480/у, ((480/у)-20)×(у+4)=480, ((480-20у)/у)×(у+4)=480, (480-20у)×(у+4)=480у, 480у+1920-20у^2-80у=480у, -20у^2-80у+1920=0, -у^2-4у+96=0, D=(-4)^2-4×(-1)×96=16+384=400, у1=(4-корень с 400)/(2×(-1))=(4-20)/(-2)=(-16)/(-2)=8, у2=(4+корень с 400)/(2×(-1))=(4+20)/(-2)=24/(-2)=-12. у2=-12 - не может быть ответом задачи, так как время не может быть отрицательным. Значит у=8, х=480/8=60. Имеем: скорость пассажирского поезда равна 60 км/ч, скорость товарно поезда равна 60-20=40 км/ч.
а) n-ый член геометрической прогрессии ищется по формуле:
Тогда пятый член этой прогрессии равен:
б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
Тогда сумма первых восьми членов этой прогрессии равна:
г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:
Тогда
А) -36; - 12; -4;
Сумма бесконечно уб. г.п.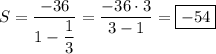
Б)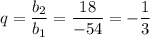
Сумма бесконечно убывающей геометрической прогрессии:
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
Так как по условию q>0, то q=3
Сумма первых восьми членов этой прогрессии равна: