Для начала найдём дискриминант, чтобы найти количество корней данного квадратного уравнения. Если , то уравнение имеет 2 корня, если , то уравнение не имеет корней. (если , то уравнение имеет 1 корень)
Поскольку , то данное квадратное уравнение имеет 2 корня. Найдём эти корни, следуя формулам.
Вспоминаем правило: из отрицательных чисел больше то, которое расположено ближе к нулю. Т.к. число расположено ближе к нулю, то .
Для начала найдём дискриминант, чтобы найти количество корней данного квадратного уравнения. Если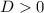 , то уравнение имеет 2 корня, если
, то уравнение имеет 2 корня, если 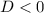 , то уравнение не имеет корней. (если
, то уравнение не имеет корней. (если 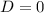 , то уравнение имеет 1 корень)
, то уравнение имеет 1 корень)
Поскольку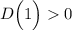 , то данное квадратное уравнение имеет 2 корня. Найдём эти корни, следуя формулам.
, то данное квадратное уравнение имеет 2 корня. Найдём эти корни, следуя формулам.
Вспоминаем правило: из отрицательных чисел больше то, которое расположено ближе к нулю. Т.к. число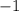 расположено ближе к нулю, то
расположено ближе к нулю, то 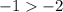 .
.
ответ:нахождение корней приведенного квадратного уравнения х²+3х+2=0 методом подбора, по теореме Виета
Используем формулы:
х₁+х₂=-p
x₁*x₂=q
х²+3х+2=0
p=3
q=2
x₁+x₂=-3 => x₁=--1; x₂=-2 -1+(-2)=-3
x₁*x₂=2 => x₁=-1; x₂=-2 (-1)*(-2)=2
нахождение корней с разложения квадратного трехчлена х²+3х+2=0 на множители
х²+3х+2 =
(х²+х)+(2х+2)= Теперь можно вынести общие множители за скобку
х(х+1)+(2(х+1)=
(х+2)(х+1)=0
Тогда:
или х+2=0 => x=-2
или х+1=0 => x=-1
x₁=-2
x₂=-1
решение квадратного уравнения через D (дискриминат) - дан в ответе другого пользователя.
Больший корень - х=-1, так как -2 < -1
ответ: х₁=-1; х₂-2