Окончание одно числа в какой-то степени рано или поздно повторяются.
3¹ = 3
3² = 9
3³ = 27
3⁴ = 81
3⁵ = 243
3⁶ = 729
Как видно окончания уже повторяются, это кстати следует из последней цифры числа вот стало окончание 3, дальше точно будет 3·3=9 и потом 9·3=27 (7). Но почему же будет окончание 3 или другое повторяющееся в первый раз? Дело в том, что всего может быть 10 цифр в окончании и рано или поздно цифра повторится. Так вот.
3 в степени 1903, как мы выяснили у тройки окончание повторяются с периодом 4.
Окончание одно числа в какой-то степени рано или поздно повторяются.
3¹ = 3
3² = 9
3³ = 27
3⁴ = 81
3⁵ = 243
3⁶ = 729
Как видно окончания уже повторяются, это кстати следует из последней цифры числа вот стало окончание 3, дальше точно будет 3·3=9 и потом 9·3=27 (7). Но почему же будет окончание 3 или другое повторяющееся в первый раз? Дело в том, что всего может быть 10 цифр в окончании и рано или поздно цифра повторится. Так вот.
3 в степени 1903, как мы выяснили у тройки окончание повторяются с периодом 4.
_ - знак окончания в моём решении ;)
_3¹⁹⁰³ = _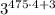 = _3³ = 7
= _3³ = 7
ответ: 7.
7
Объяснение:
81≡1(mod10)⇒81⁴⁷⁵≡1⁴⁷⁵≡1(mod10)
27≡7(mod10)
3¹⁹⁰³=(3⁴)⁴⁷⁵·3³=81⁴⁷⁵·27≡1·7≡7(mod10)