Объяснение:
№1
А) (2х+1)²= 4х²+4х+1
Б) (3а-с)²= 9а²–6ас+с²
В) (а+6)(а-6)= а²–36
Г) (3х-4у) (3х+4у)= 9х²–16у²
№2
А) у²-¼= (у–½)(у+½)
Б) х²+10х+25= (х+5)²
№3
(2х-у)²-4х(х-у)= 4х²–4ху+у²–4х²+4ху= у²
при у= -⅔
(–⅔)²=
ответ:
№4
А) 3(2а-b) (2a+b)= 3(4a²–b²)= 12a²–3b²
Б (х⁴+у³)² = (x^8)+2x⁴y³+(y^6)
В) (а+3b)²-(a-3b)²=(a+3b+a–3b)(a+3b–(a–3b))= a²(a+3b–a+3b)= a²*6b= 6a²b
№5
А) (2а-5)²-(2а-3) (2а+3)=0
(4a²–20a+25)–(4a²–9)=0
4a²–20a+25–4a²+9=0
–20a+34=0
20a=34
a=
a= 1,7
Б) 9с²-25=0
(3c–5)(3c+5)=0
совокупность:
3с–5=0
3с+5=0
3с=5
3с=–5
с=
Объяснение:
№1
А) (2х+1)²= 4х²+4х+1
Б) (3а-с)²= 9а²–6ас+с²
В) (а+6)(а-6)= а²–36
Г) (3х-4у) (3х+4у)= 9х²–16у²
№2
А) у²-¼= (у–½)(у+½)
Б) х²+10х+25= (х+5)²
№3
(2х-у)²-4х(х-у)= 4х²–4ху+у²–4х²+4ху= у²
при у= -⅔
(–⅔)²=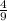
ответ: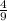
№4
А) 3(2а-b) (2a+b)= 3(4a²–b²)= 12a²–3b²
Б (х⁴+у³)² = (x^8)+2x⁴y³+(y^6)
В) (а+3b)²-(a-3b)²=(a+3b+a–3b)(a+3b–(a–3b))= a²(a+3b–a+3b)= a²*6b= 6a²b
№5
А) (2а-5)²-(2а-3) (2а+3)=0
(4a²–20a+25)–(4a²–9)=0
4a²–20a+25–4a²+9=0
–20a+34=0
20a=34
a=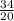
a= 1,7
Б) 9с²-25=0
(3c–5)(3c+5)=0
совокупность:
3с–5=0
3с+5=0
совокупность:
3с=5
3с=–5
совокупность:
с=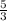
с=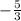
совокупность:
с=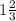
с=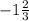
1) Рассмотрим ромб АВСD. У него BD и АС - пересекающиеся диагонали. У ромба диагонали пересекаются под прямым углом, и точкой пересечения делиться пополам, значит ВO = 1/2 BD = 12 * 1/2 = 6 *(сm).
2) Рассмотрим треугольник АОВ. Он прямоугольный (угол О = 90 град.), значит по теореме Пифагора:
АО^2 + BO^2 = AB^2
AO^2 + 6^2 = 10^2
AO^2 = 100 - 36
AO^2 = 64
AO = корень из 64
AO(маленькая 1 снизу) = 8 (см), АО(маленькая 2 снизу) = -8 - не удовлетворяет условие задачи.
3) S (ABCD) = 1/2*AO*BO
S (ABCD) = 1/2 * 8 * 6
S (ABCD) = 1/2 * 48
S (ABCD) = 24 см^2
ответ: 24 см^2