Если выразить из основного тригонометрического тождества квадрат синуса и подставить в данную формулу, то получится еще одна формула косинуса двойного угла:
Аналогично, можно вывести еще одну формулу:
В данном случае удобно использовать формулу , так как найти косинус двойного аргумента нужно, зная только косинус одинарного аргумента.
Преобразуем выражение, используя формулу косинуса двойного аргумента:
Косинус двойного аргумента:
Если выразить из основного тригонометрического тождества квадрат синуса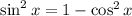
и подставить в данную формулу, то получится еще одна формула косинуса двойного угла:
Аналогично, можно вывести еще одну формулу:
В данном случае удобно использовать формулу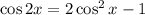
, так как найти косинус двойного аргумента нужно, зная только косинус одинарного аргумента.
Преобразуем выражение, используя формулу косинуса двойного аргумента:
ответ: 3.32