В переписке всё-таки выяснилось, что не a^3+b^3=91, а a^3+27b^3=91.
Итак,
Раскрыв , мы имеем
Это выражение можно получить, сложив первое заданное уравнение со вторым, умноженным на 9:
Получаем:
Откуда
ответ: a+ 3b = 7.
В переписке всё-таки выяснилось, что не a^3+b^3=91, а a^3+27b^3=91.
Итак,
Раскрыв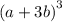 , мы имеем
, мы имеем
Это выражение можно получить, сложив первое заданное уравнение со вторым, умноженным на 9:
Получаем:
Откуда
ответ: a+ 3b = 7.