1.
2x-5y при x=7; y=3
2×7-5×3
14-15= -1
ответ: -1
2.
3+2a = -3+2a при a=11
3+3= -2а+2а
6=0 не тождество т.к 6> 0
ответ: 3+2a > -3+2a
3.
1) 8y-4,4y = 3,6у
2)15a-a+b-6b = 15а-1а+1b-6b=14a+(-5b) = 14a-5b
3)2a+(3a-8b)= 2a+3a-8b = 5a-8b
4)(5-2b)-(7+10b) = 5-2b-7-10b = 5-7-2b-10b =-2-12b
5)(2-4b)-(31b-6)-11 = 2-4b-31b+6-11 = 2+6-11-4b-31b = -3-35b
4.
1)3x+2=0
3x=0-2
3x= -2
x= -2/3
2)8x-5=x-40
8х-х=5-40
7х=-35
х=5
3)6x+(3x-2)=14
6х+3х-2=14
9х=2+14
9х=16
х= 1 целая 7/9
объяснение:
если непонятно что-то , то напиши в комментариях
Объяснение:
4) x^2(3x + 1) - (x^2 + 1)^2 = 3
3x^3 + x^2 - x^4 - 2x^2 - 1 - 3 = 0
3x^3 - x^4 - x^2 - 4 = 0
x^4 - 3x^3 + x^2 + 4 = 0
Попробуем подобрать целые корни, они могут быть равны делителям свободного члена, т. е. 4
Проверим 1:
1 - 3 + 1 + 4 0 - не подходит
Проверим 2, 2 подходит, значит, можно выделить множитель x - 2
x^4 - 2x^3 - x^3 + 2x^2 - x^2 + 4 = 0
(x - 2)x^3 - x^2(x-2) -(x-2)(x+2) = 0
(x^3 - x^2 - x - 2)(x-2) = 0
x^3 - x^2 - x - 2 = 0
Здесь также подходит корень x = 2, выделим множитель x - 2
x^3 - 2x^2 + x^2 - 2x + x - 2 = 0
x^2(x-2) + x(x - 2) +(x - 2) = 0
(x^2 + x + 1)(x - 2) = 0
x^2 + x + 1 = 0
D = 1 - 4*1*1 = -3 - нет действительных корней
Получается, действительный корень только x = 2
2) (2x^2 - 1)^2 + x(2x - 1)^2 = (x + 1)^2 + 16x^2 - 6
4x^4 - 4x^2 + 1 + 4x^3 - 4x^2 + x = x^2 + 2x + 1 + 16x^2 - 6
4x^4 + 4x^3 - 25x^2 - x + 6 = 0
Подбираем корни - делители 6
x = 1 и x = -1 не подходит
x = 2 - подходит
4*16 + 4*8 - 100 - 2 + 6 = 96 - 100 - 2 + 6 = 0
Множитель x - 2
4x^4 - 8x^3 + 12x^3 - 24x^2 - x^2 + 2x - 3x + 6 = 0
(x - 2)(4x^3 + 12x^2 - x - 3) = 0
4x^3 + 12x^2 - x - 3 = 0
Подбираем корни - делители 3
x = -3 подходит
4 * (-27) + 12*9 + 3 - 3 = -108 + 108 = 0
Множитель x - (-3) = x + 3
4x^2(x + 3) - (x + 3) = 0
(2x - 1)(2x + 1)(x + 3) = 0
2x - 1 = 0 ⇒ x = 0.5
2x + 1 = 0 ⇒ x = -0.5
Итого 4 действительных корня x = 0.5, x = -0.5, x = -3, x = 2
1.
2x-5y при x=7; y=3
2×7-5×3
14-15= -1
ответ: -1
2.
3+2a = -3+2a при a=11
3+3= -2а+2а
6=0 не тождество т.к 6> 0
ответ: 3+2a > -3+2a
3.
1) 8y-4,4y = 3,6у
2)15a-a+b-6b = 15а-1а+1b-6b=14a+(-5b) = 14a-5b
3)2a+(3a-8b)= 2a+3a-8b = 5a-8b
4)(5-2b)-(7+10b) = 5-2b-7-10b = 5-7-2b-10b =-2-12b
5)(2-4b)-(31b-6)-11 = 2-4b-31b+6-11 = 2+6-11-4b-31b = -3-35b
4.
1)3x+2=0
3x=0-2
3x= -2
x= -2/3
2)8x-5=x-40
8х-х=5-40
7х=-35
х=5
3)6x+(3x-2)=14
6х+3х-2=14
9х=2+14
9х=16
х= 1 целая 7/9
объяснение:
если непонятно что-то , то напиши в комментариях
Объяснение:
4) x^2(3x + 1) - (x^2 + 1)^2 = 3
3x^3 + x^2 - x^4 - 2x^2 - 1 - 3 = 0
3x^3 - x^4 - x^2 - 4 = 0
x^4 - 3x^3 + x^2 + 4 = 0
Попробуем подобрать целые корни, они могут быть равны делителям свободного члена, т. е. 4
Проверим 1:
1 - 3 + 1 + 4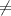
0 - не подходит
Проверим 2, 2 подходит, значит, можно выделить множитель x - 2
x^4 - 2x^3 - x^3 + 2x^2 - x^2 + 4 = 0
(x - 2)x^3 - x^2(x-2) -(x-2)(x+2) = 0
(x^3 - x^2 - x - 2)(x-2) = 0
x^3 - x^2 - x - 2 = 0
Здесь также подходит корень x = 2, выделим множитель x - 2
x^3 - 2x^2 + x^2 - 2x + x - 2 = 0
x^2(x-2) + x(x - 2) +(x - 2) = 0
(x^2 + x + 1)(x - 2) = 0
x^2 + x + 1 = 0
D = 1 - 4*1*1 = -3 - нет действительных корней
Получается, действительный корень только x = 2
2) (2x^2 - 1)^2 + x(2x - 1)^2 = (x + 1)^2 + 16x^2 - 6
4x^4 - 4x^2 + 1 + 4x^3 - 4x^2 + x = x^2 + 2x + 1 + 16x^2 - 6
4x^4 + 4x^3 - 25x^2 - x + 6 = 0
Подбираем корни - делители 6
x = 1 и x = -1 не подходит
x = 2 - подходит
4*16 + 4*8 - 100 - 2 + 6 = 96 - 100 - 2 + 6 = 0
Множитель x - 2
4x^4 - 8x^3 + 12x^3 - 24x^2 - x^2 + 2x - 3x + 6 = 0
(x - 2)(4x^3 + 12x^2 - x - 3) = 0
4x^3 + 12x^2 - x - 3 = 0
Подбираем корни - делители 3
x = -3 подходит
4 * (-27) + 12*9 + 3 - 3 = -108 + 108 = 0
Множитель x - (-3) = x + 3
4x^2(x + 3) - (x + 3) = 0
(2x - 1)(2x + 1)(x + 3) = 0
2x - 1 = 0 ⇒ x = 0.5
2x + 1 = 0 ⇒ x = -0.5
Итого 4 действительных корня x = 0.5, x = -0.5, x = -3, x = 2