Сложим первое уравнение,домноженное на 2 со вторым:
Очевидно,что x и y не обращаются в ноль,так как число 19 простое и не имеет делителей на интервале (1;19)
Значит:
Из полученных отрезков лишь пара значений модулей удовлетворяет нашему уравнению:
Осталось лишь раскрыть модуль,сделаем это следующим образом:
Рассмотрим полиномы вида:
Подставим модули корней под степени 2,так как они являются четными и не меняют значение:
Очевидно,что для старших мономов вида обоих полиномов для обращения последних в ноль определен отрицательный знак.Это выполнимо в случае только одного отрицательного и одного положительного переменного.
Значит возможные целочисленные значения решения исходной системы:
Сложим первое уравнение,домноженное на 2 со вторым:
Очевидно,что x и y не обращаются в ноль,так как число 19 простое и не имеет делителей на интервале (1;19)
Значит:
Из полученных отрезков лишь пара значений модулей удовлетворяет нашему уравнению:
Осталось лишь раскрыть модуль,сделаем это следующим образом:
Рассмотрим полиномы вида:
Подставим модули корней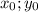 под степени 2,так как они являются четными и не меняют значение:
под степени 2,так как они являются четными и не меняют значение:
Очевидно,что для старших мономов вида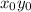 обоих полиномов для обращения последних в ноль определен отрицательный знак.Это выполнимо в случае только одного отрицательного и одного положительного переменного.
обоих полиномов для обращения последних в ноль определен отрицательный знак.Это выполнимо в случае только одного отрицательного и одного положительного переменного.
Значит возможные целочисленные значения решения исходной системы: