Найдите дисперсию и стандартное наклонение
Алгебра 8 кл

Найдите дисперсию и стандартное наклонение Алгебра 8 кл

Показать ответ

Ответ:

Maria123456789101

27.01.2021 03:52

1. ОТВЕТ: например,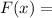 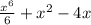F(x)= $\frac{x^6}{6}+x^2-4x$ , поскольку F'(x) = f(x) .

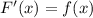Общий вид первообразных -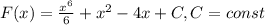 $F(x)=\frac{x^6}{6}+x^2-4x+C, C=const$

2. Докажем, что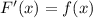 F'(x)=f(x) :

$F'(x)=(2\sin x+3x)'=2(\sin x)'+3x'=2\cos x+3=f(x)$ .

Что и требовалось доказать.

3. Общий вид первообразных функции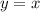 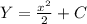y=x - $Y=\frac{x^2}{2}+C$ , где 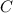- некоторое постоянное число. Если график первообразной проходит через точку 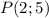P(2;5) , то это значит, что при подстановке 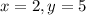x=2, y=5 получим верное равенство:

$5=\frac{2^2}{2}+C;\\\\5=2+C\Rightarrow C=3.$

Искомая первообразная -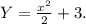 $Y=\frac{x^2}{2}+3.$

ОТВЕТ: Y = x²/2 + 3.

4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.

Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид

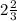$S=\int\limits^2_0 {(4x-x^2-x^2)} \, dx =\int\limits^2_0 {(4x-2x^2)} \, dx =(2x^2-\frac{2x^3}{3})|^2_0=(2\cdot2^2-\frac{2\cdot2^3}{3})-(2\cdot0^2-\frac{2\cdot0^3}{3})=8-\frac{16}{3}=8-5\frac{1}{3}=2\frac{2}{3}.$

ОТВЕТ: $2\frac{2}{3}$ кв. ед.

5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.

Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид

$S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12$

ОТВЕТ: 12 кв. ед.

6. Объем выполненной работы A(t) с момента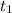 t_1 по момент 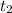t_2 согласно механическому смыслу определенного интеграла есть значение выражения интеграла

$\int\limits^{t_2}_{t_1} {f(t)} \, dt$

Имеем:

$A(t)=\int\limits^5_0 {(-2,53t^2+24,75t+111,1)} \, dt=(\frac{-2,53t^3}{3}+\frac{24,75t^2}{2}+111,1t)|_0^5=-\frac{253\cdot5^3}{300}+\frac{2475\cdot5^2}{200}+111,1\cdot5\approx760$

ОТВЕТ: ≈ 760.

Интеграл и его применение 1.Найти первообразную для функции f(x)=x5 +2x-4 2. Доказать, что функция

0,0(0 оценок)

Ответ:

Лейля16

16.04.2020 12:50

(а+1)во 2 степени-(2а+3)во 2 степени=0
Нужно раскрыть скобки по формулам сокращенного умножения
Сначала раскроем (а+1)во второй степени,получится
а в квадрате +2а+1
Дальше рассмотрим оставшиеся,то есть -(2а+3)во второй степени
-(4а в квадрате +12а+9 )
Раскроем скобки и получится
-4а в квадрате -12а-9
В итоге получилось
а в квадрате +2а+1-4а в квадрате -12а-9
Находим подобные и получается
-3 а в квадрате -10 а -8=0
Теперь решаем дискриминантом
Д(дискриминант)=корню из четырех ,то есть двум
А1= -2 целые одна третья
А2= -1

Второе уравнение решается аналогично
25 с в квадрате +80с +64 -с в квадрате +20с-100=0
Что-бы было удобней вычитать Д сократим все на два,и получится
6с в квадрате+25с-9=0
Д=корень из 841 =29
С1=1/3
С2=11/3=3 целых 2/3

0,0(0 оценок)

Популярные вопросы: Алгебра