Найдите допустимые значения переменной в выражение
Только с объяснениями ​

См. Объяснение

Объяснение:

Это связано с тем, какой общий знаменатель у этих трёх дробей.

Чтобы найти общий знаменатель, необходимо:

1) знаменатель каждой дроби разложить на множители:  

а) знаменатель первой дроби уже представлен в виде произведения;

b) знаменатель второй дроби: (1+z)² = (1+z)·(1+z)

с) знаменатель третьей дроби: (1-z)² = (1-z)·(1-z)

2) находим общий знаменатель - такое наименьшее выражение, которое делится на знаменатель каждой из 3-х дробей:

Общий знаменатель = (1-z)·(1+z)·(1+z)·(1-z) = (1+z)²·(1-z)²

Здесь (1-z)·(1+z) - от первой дроби; (1+z) добавили от 2-й дроби, чтобы общий знаменатель делился на (1+z)²; (1-z) добавили от 3-й дроби, чтобы общий знаменатель делился на (1-z)².

3) находим дополнительные множители:

а) к первой дроби:

(1-z)·(1+z)·(1+z)·(1-z) : (1-z)·(1+z) = (1+z)·(1-z)

b) ко второй дроби:

(1-z)·(1+z)·(1+z)·(1-z) : (1+z)·(1+z) = (1-z)·(1-z) = (1-z)²

с) к третьей дроби:

(1-z)·(1+z)·(1+z)·(1-z) : (1-z)·(1-z) = (1+z)·(1+z) = (1+z)²  

4) после перемножения получаем в числителе:

3 · (1+z)·(1-z) - 2 · (1-z)²  + 5 · (1+z)²

Один  корень

Объяснение:

Левая часть -  положительна , значит положительна и правая ,  

  то есть x > 0  ,   но  тогда функция , стоящая в левой части - возрастает

( как сложная  функция , составленная  их двух  возрастающих )  , а  в

правой части - убывающая функция , значит уравнение может иметь не

более одного корня  ;  

Функция y =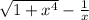    непрерывна  при x > 0  ;          

 y ( 0,1 ) =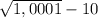 <  0  ;   y (1) =    ⇒    

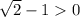на интервале ( 0 ; 1 )   y (x)   имеет корень  и как доказано  он

 единственный