Объяснение:
1) 0,5·sin2x = sin35° ⇔ sin2x = 2·sin35° (1) ; так как y = sinx
возрастает в первой четверти , то sin35° > sin30° = 0,5 ⇒
2·sin35° > 1 ⇒ уравнение (1) не имеет решений
2) arcsin 2x = arccos x (2) , arccos x ≥ 0 для всех х ⇒ arcsin 2x ≥ 0
⇒ х ≥ 0 ; так как из области определения у = arcsin2x следует
, что х ≤ 0,5 , то уравнение (2) имеет решение только ,
если x ∈ [ 0 ; 0,5] , на этом отрезке левая часть уравнения
меняется от 0 до π/2 , а правая от π/3 до π/2 ⇒
уравнение ( 2) имеет решение , если множество
значений обеих частей не выходит за пределы [π/3 ; π/2] , но
на этом отрезке функция y = sinx - возрастает ⇒ уравнение ( 1 )
равносильно на [ 0 ; 0,5] следующему :
sin(arcsin2x) = sin(arccosx)
2x = ⇔ 4x² = 1 - x² ⇔ x² = 1/5 ⇒
x = ( так как х ≥ 0)
функции , стоящие в левой и правой частях уравнения имеют
разную монотонность , поэтому сразу ясно , что уравнение
имеет не более одного корня , в этом случае его достаточно
" угадать " , но угадать не получилось , пришлось брать
синусы от обеих частей
f(x) = g(x) ⇔ h(f(x)) = h(g(x) ) , если h(x) - монотонна и значения
f и g входят в область определения функции h , поэтому
и пришлось доказывать , что значения f и g не выходят
за пределы первой четверти , а там синус возрастает и
поэтому законно брать синусы от обеих частей
Объяснение:
1) 0,5·sin2x = sin35° ⇔ sin2x = 2·sin35° (1) ; так как y = sinx
возрастает в первой четверти , то sin35° > sin30° = 0,5 ⇒
2·sin35° > 1 ⇒ уравнение (1) не имеет решений
2) arcsin 2x = arccos x (2) , arccos x ≥ 0 для всех х ⇒ arcsin 2x ≥ 0
⇒ х ≥ 0 ; так как из области определения у = arcsin2x следует
, что х ≤ 0,5 , то уравнение (2) имеет решение только ,
если x ∈ [ 0 ; 0,5] , на этом отрезке левая часть уравнения
меняется от 0 до π/2 , а правая от π/3 до π/2 ⇒
уравнение ( 2) имеет решение , если множество
значений обеих частей не выходит за пределы [π/3 ; π/2] , но
на этом отрезке функция y = sinx - возрастает ⇒ уравнение ( 1 )
равносильно на [ 0 ; 0,5] следующему :
sin(arcsin2x) = sin(arccosx)
2x =
⇔ 4x² = 1 - x² ⇔ x² = 1/5 ⇒
x =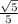
( так как х ≥ 0)
функции , стоящие в левой и правой частях уравнения имеют
разную монотонность , поэтому сразу ясно , что уравнение
имеет не более одного корня , в этом случае его достаточно
" угадать " , но угадать не получилось , пришлось брать
синусы от обеих частей
f(x) = g(x) ⇔ h(f(x)) = h(g(x) ) , если h(x) - монотонна и значения
f и g входят в область определения функции h , поэтому
и пришлось доказывать , что значения f и g не выходят
за пределы первой четверти , а там синус возрастает и
поэтому законно брать синусы от обеих частей
9(1-cos²α)-4=9(1-(-2\9)²)-4=9(1-4\81)-4=9·77\81-4=77\9-4=8 .5\9-4=4. 5\9
2)7-5cos²α sinα=3\5 cos²α=1-sin²α
7-5(1-sin²α)=7-5(1-(3\5)²)=7-5(1-9\25)=7-5·16\25=7-16\5=7-3. 1\5=3.4\5
3) 10cos²α-sin²α cos²α=3\5
10cos²α-(1-cos²α)=10cos²α-1+cos²α=11cos²α-1
11·3\5-1=33\5-1=28\5=5. 3\5
4) sinα=-3\7 cos2α=?
cos2α=cos²α-sin²α cos²α=1-sin²α
cos²α=1-(-3\7)²=1-9\49=40\49
cos2α=40\49-9\49=31\49
5) sin2α·sin3α-cos2α·cos3α-cos5α=-cos(2α+3α)-cos5α=-2cos5α
6) Решить уравнение:
1) tg3x=1
3x=π\4+πn n∈Z
x=π\12+πn\3 n∈Z
2)sin(2x-π\6)=-1
2x-π\6=-π\2+2πk k∈Z
2x=-π\2+π\6+2πk k∈Z
2x=-π\3+2πk k∈Z
x=-π\6+πk k∈Z