Найдите двадцать третий член арифметической прогрессии(an) , если а1=-15иd=3. Найдите сумму шестнадцати первых членов арифметической пронрессии:8; 4; 0; Найдите сумму шестидесяти первых членов последовательности (bn)заданой формулой bn=3n-1 Является ли число 54,5 членом арифметической прогрессии (an), в которой a1=25,5 и а9=5,5? Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих

Показать ответ

Ответ:

dog126

24.03.2022 11:41

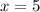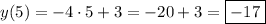
1. Известно, что x=5 , $y(5)=-4\cdot 5+3=-20+3=\boxed{-17}$

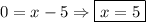
2. Известно, что y=0 , тогда $0=x-5\Rightarrow \boxed{x=5}$

3. Обе точки имеют координаты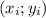 (x_i; y_i) , причем при подставлении этих координат в уравнение функции, мы получаем верное равенство.

Смотрим на точку А: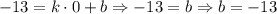 $-13= k\cdot 0+b \Rightarrow -13=b\Rightarrow b=-13$

Отлично, уравнение известно теперь в таком виде: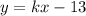 y=kx-13 , в него подставим вторую точку и найдем .

$\displaystyle 0=-\frac{13}{8}\cdot k-13\Rightarrow 13=-\frac{13}{8}\cdot k \bigg|\cdot\bigg(-\frac{8}{13} \bigg) \Rightarrow -8=k\Rightarrow \boxed{k=-8}$

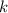4. Решаем аналогично. Точка А: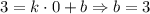 $3 = k\cdot 0+b\Rightarrow b=3$

Уравнение уже в виде: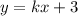 y=kx+3

Точка B: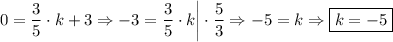 $\displaystyle 0=\frac{3}{5}\cdot k+3\Rightarrow -3=\frac{3}{5}\cdot k\bigg|\cdot \frac{5}{3} \Rightarrow -5=k\Rightarrow \boxed{k=-5}$

5. Условие симметрии относительно прямой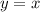 y=x такое, что у функции 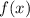f(x) меняются местами область определения и область значений, то есть подставляя 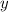вместо мы получаем по итогу . При взаимно однозначном соответствии области определения и области значений (как в случае прямых) все вообще просто и работает везде.

Что нужно сделать: есть y=2x+1 , делаем

$\displaystyle x=2y+1\Rightarrow 2y=x-1\Rightarrow \boxed{y=\frac{x}{2}-\frac{1}{2} }$

0,0(0 оценок)

Ответ:

Okean111

30.06.2022 00:50

1)
sin2x -cos²x =0 ;
2sinx*cosx -cos²x =0 ;
cosx(2sinx-cosx) =0 ;
[cosx =0 ; 2sinx-cosx=0⇒x=π/2+πn , x =arcctq2 ; n∈Z.

2)
cos2x +cos²x =0 ;
cos²x - sin²x+cos²x =0 ;
sin²x =0 ⇒sinx =0 ;
x =πn , n∈Z.

3).
2cos⁴x+3cos²x-2=0 ;
* * * замена переменной t = cos²x ; 0≤ t ≤ 1 * * *
2t²+3t-2=0 ; * * * D =3² -4*2*(-2) =25 =5² * * *
t₁ = (-3 -5)/4 = -2 не удов. 0≤ t ≤ 1.
t₂ =(-3+5)/4 =1/2⇒cos²x =1/2⇔(1+cos2x)/2 =1/2⇔cos2x=0 ⇒
2x =π/2+ πn , n∈Z ;
x = π/4+ (π/2)*n , n∈Z.

4).
2cos²x+5sinx-4=0 ;
2(1-sin²x)+5sinx-4=0 ;
2sin²x-5sinx+2=0 ; * * * D =5² -4*2*2 =25 =3² * * *
sinx = (5+3)/4 =2 не умеет решения ;
sinx = (5-3)/4 =1/2 ⇒ x =(-1)^n *(π/6) + πn , n∈Z .

5). 2cos^2x(3p/2-x)-5sin(p/2-x)-4=0 ;
2cos²(3π/2-x)-5sin(π/2-x)-4=0 ;
2sin²x -5cosx -4 = 0 ;
2(1-cos²x) -5cosx -4 = 0 ;
2cos²x +5cosx +2 = 0 ; * * *D =5² -4*2*2 =25 =3² * * *
cos²x +(2+1/2)cosx +1 = 0 ⇒[cosx =2 ; cosx =1/2 .
cosx =1/2 ;

x =±π/3 +2πn , n∈Z .

0,0(0 оценок)

Популярные вопросы: Алгебра