Проверим, является ли левая часть полным дифференциалом некоторой функции u(x, y). Пусть P = x²y² + y, Q = 2x³y - x. Левая часть является полным дифференциалом, если :
Левая часть не является полным дифференциалом. Подберём интегрирующий множитель такой, чтобы при домножении на него обеих частей уравнения выполнялось равенство , то есть левая часть стала полным дифференциалом. Так как мы ищем функцию от x, при дифференцировании по y мы считаем её, как константу:
При домножении на t получаем:
Это уравнение в полных дифференциалах. Подберём функцию u(x, y) такую, что . Из определения дифференциала функции двух переменных следует, что — частная производная по x. Тогда , где — константа, зависящая от y (поскольку функция была от двух переменных, а проинтегрировали мы только по x). Также из определения дифференциала:
Тогда , решение уравнения:
При x = 1, y = 1 получаем C = 0. Выразим y через x:
4
Объяснение:
Проверим, является ли левая часть полным дифференциалом некоторой функции u(x, y). Пусть P = x²y² + y, Q = 2x³y - x. Левая часть является полным дифференциалом, если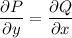 :
:
Левая часть не является полным дифференциалом. Подберём интегрирующий множитель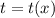 такой, чтобы при домножении на него обеих частей уравнения выполнялось равенство
такой, чтобы при домножении на него обеих частей уравнения выполнялось равенство 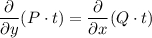 , то есть левая часть стала полным дифференциалом. Так как мы ищем функцию от x, при дифференцировании по y мы считаем её, как константу:
, то есть левая часть стала полным дифференциалом. Так как мы ищем функцию от x, при дифференцировании по y мы считаем её, как константу:
При домножении на t получаем:
Это уравнение в полных дифференциалах. Подберём функцию u(x, y) такую, что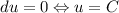 . Из определения дифференциала функции двух переменных следует, что
. Из определения дифференциала функции двух переменных следует, что 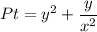 — частная производная по x. Тогда
— частная производная по x. Тогда 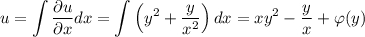 , где
, где 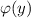 — константа, зависящая от y (поскольку функция была от двух переменных, а проинтегрировали мы только по x). Также из определения дифференциала:
— константа, зависящая от y (поскольку функция была от двух переменных, а проинтегрировали мы только по x). Также из определения дифференциала:
Тогда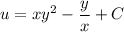 , решение уравнения:
, решение уравнения: 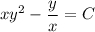
При x = 1, y = 1 получаем C = 0. Выразим y через x:
В точке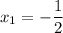 значение функции равно 4.
значение функции равно 4.