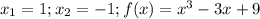и , то
и - точки экстремума функции, производная которой
,
и
в точках и :
, то
и - точки экстремума функции центрально- симметричные относительно начала координат, значит = -
⇒
Решаем систему :
Складываем первые два уравнения и вычитаем:
О т в е т.
и
и
⇒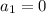
Решаем систему :
Складываем первые два уравнения и вычитаем:
О т в е т.