Найдите коэффициент при 2 в биномиальном разложении (2 − 3)3​

3)x=

4)x=

Объяснение:

3)

-=

Умножаем обе части():

3(6x-1)-4(3x+1)=3

Распределить 3 и 4 через скобки:

18x-3-4(3x+1)=3

18x-3- 12x - 4=3

Привести подобные члены:

6x-3-4=3

6x-7=3

Переносим постоянную(-7) в правую часть и сменяем ее знак:

6x=3+7

Вычисляем:

6x=10

Разделим обе стороны на 6:

x=

4)

+ = 1

Раскрываем скобки:

+ = 1

Умножаем обе части уравнения на 4:

2(2x-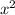)+3x+2

Распределяем 2 через скобки(2(2x-)):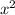

4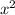x-2+3x+2

Поскольку сумма двух противоположных величин равна нулю, надо удалить их из выражения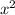(-2 и 2

4x+3x=4

7x=4

Разделить обе стороны на 7:

x=

Надеюсь

:)

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими ее можно задать:

Табличный быстро определить конкретные значения без дополнительных измерений или вычислений.

Графический — наглядно.

Аналитический — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный .

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида Область определения область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.