Найдите координаты точки пересечения двух касательных, проведенных к графику функции y=sin3x : первая в точке с абсциссой 3pi/18, вторая с абсциссой 5pi/18

25

Объяснение:

решения.

Выпишем несколько первых натуральных чисел кратных 5:

5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).

Пронумеруем члены последовательности:

Число, следующее за четвертым членом последовательности 25.

решения.

Воспользуемся формулой для нахождения n-го члена арифметической последовательности.

Наименьшее натуральное число делящееся на 5 это 5, т.е. .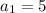

Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е. .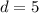

Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.

1) Чтобы значение квадратного корня было натуральным числом, подкоренное выражение должно быть полным квадратом, при этом n должно быть наименьшим (по условию).

169=13²

12²=144 - ближайший к 169 квадрат числа, значит  n=169-144=25

ответ: n=25

2) Чтобы значение квадратного корня было натуральным числом, подкоренное выражение должно быть полным квадратом, при этом n должно быть наибольшим (по условию).

121=11²  

1²=1 - наименьшее возможное  значение покоренного выражения, значит  n=121-1=120

ответ: n=120