Если t лежит в 4-й четверти, синус отрицателен, поэтому сумма синуса и косинуса не может равняться 1 (ведь оба они лежат в пределах между минус 1 и 1). Поэтому Если t=0, то cos t=1, sin t=0, то есть t=0 является решением. Если
то есть на этом промежутке решений нет. Поэтому единственное решение t=0, откуда x=0.
Если t лежит в 4-й четверти, синус отрицателен, поэтому сумма синуса и косинуса не может равняться 1 (ведь оба они лежат в пределах между минус 1 и 1). Поэтому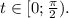 Если t=0, то cos t=1, sin t=0, то есть t=0 является решением. Если
Если t=0, то cos t=1, sin t=0, то есть t=0 является решением. Если
то есть на этом промежутке решений нет. Поэтому единственное решение t=0, откуда x=0.
ответ: 0