Найдите многочлен, равный произведению одночлена и многочлена и объясните свой выбор: а) 3 и ( а + б ) б) х и ( а - б ) в) ( х+1) и 5 г) ( а - б) и х д) ( а + 3) 7 е) ( х - у) 10 ё) а ( х- у) ж) а ( а +б) з) (а + б - с) 2 и) ( а - б ) ( - 6)
График - парабола с вершиной в точке (5;1) , ветви вверх, ось симметрии х=5 . Получена из параболы путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
Пересечение с осью ОХ нет ⇒ при .
Пресечение с осью ОУ в точке .
Убывает при , возрастает при .
Точка минимума минимальное значение функции .
График - парабола, с вершиной в точке (2;-3) , ветви вверх, ось симметрии х= -2 . Получена при перемещении графика вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .
ответы в решениях.
Объяснение:
1) x²+2x-24=0;
По теореме Виета
x1+x2=-2; x1*x2=-24;
x1=4; x2=-6.
***
2) x²-9x+20=0;
x1+x2=9; x1*x2=20;
x1=5; x2=4.
***
3) 10n²-9n+2=0;
a=10; b=-9; c=2.
D=b²-4ac=(-9)²-4*10*2=81-80=1>0 - 2 корня.
x1=(-b+√D)/2a=(-(-9)+√1)/2*10=8/20 = 0.4;
x2=(-b-√D)/2a=(-(-9)-√1)/2*10= 10/20= 1/2 = 0.5.
***
4) 21y²-2y-3=0;
a=21; b=-2; c=-3;
D=256>0 - 2 корня.
y1=0.428; y2=0.333.
***
5) x²+8x-13=0;
x1+x2=-8; x1*x2=-13;
x1=1,38; x2=-9,38.
***
6)2x²-4x-17=0;
a=2; b=-4; c=-17;
D= 152 >0 - 2 корня.
x1=4,08; x2= -2,08.
***
7) 9x²+42x+49=0;
a=9; b=42; c=49;
D=0 - 1 корень;
x=-b/2a=-42/2*9=-42/18 = -2,33.
***
8) x²-10x+37=0;
a=1; b=-10; c=37;
D= -48 - нет корней.
График - парабола с вершиной в точке (5;1) , ветви вверх, ось симметрии х=5 . Получена из параболы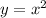 путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
Пересечение с осью ОХ нет ⇒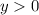 при
при 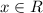 .
.
Пресечение с осью ОУ в точке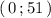 .
.
Убывает при![x\in (-\infty ;\, 5\ ]](/tpl/images/1657/0857/c774b.png) , возрастает при
, возрастает при 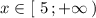 .
.
Точка минимума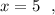 минимальное значение функции
минимальное значение функции 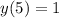 .
.
График - парабола, с вершиной в точке (2;-3) , ветви вверх, ось симметрии х= -2 . Получена при перемещении графика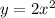 вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .
вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .