Найдите наибольшее и наименьшее значение фнукции инарисуйте график y=sin(x+pi/3)-1

Сначала просто решим неравенство методом интервалов:
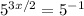Найдём корни числителя:
;
3x/2=-1;
x= -2/3;
Найдём корни знаменателя:
x-4=0;
x=4;

Теперь начертим числовую прямую, отметим на ней точки -2/3 и 4 и посмотрим, где всё выражение принимает значения больше нуля (числовая прямая прикреплена).
Мы видим, что всё выражение больше нуля при x>4 и x< -2/3
Поскольку нам нужен наименьшее целое положительное решение, мы берём число 5 (4 мы взять не можем, т.к. в знаменателе будет 0 и потому, что 4 не входит в получившиеся лучи). 
ответ: 5. 

1) х=у-1             х=у-1                  х=у-1              х=у-1    х=у-1   х=5-1   х=4

    2х+у=13       2(у-1)+у=13      2у-2+у=13      3у=15   у=5      у=5      у=5

2)а-2в=3    а=3+2в             а=3+2в    а=3+2в   а=3+2(-17)    а=3-34       а=-31

   а-3в=20   3+2в-3в=20     -в=17        в=-17     в=-17                в=-17         в=-17

3) m+3n=2        m=2-3n                  m=2-3n              m=2-3n     m=2-3n   m=2-3(-1)     m=5

     2m+3n=7       2(2-3n) +3n=7     4-6n+3n=7         -3n=3        n=-1          n=-1              n=-1