Получаем , но рассматриваемая точка экстремума положительная, поэтому откидываем значение x = -1.
(0)__+___(1/2)____-___(1)
Вертикальная асимптота: x = 0 и учитывая то, что функция возрастает с 0(не включая) до значения x=1/2, то у функции наименьшего значения нет.
2) Если 1 < x ≤ 2, то - возрастает на промежутке x > 1. Но на промежутке x ∈ (1; 2] будет наибольшее значение функции в точке x = 2 и равно оно . Наименьшего значения функции не существует.
Область определения функции: x > 0
Рассмотрим два случая:
1) Если 0 < x < 1, то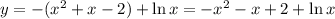
Получаем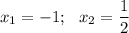 , но рассматриваемая точка экстремума положительная, поэтому откидываем значение x = -1.
, но рассматриваемая точка экстремума положительная, поэтому откидываем значение x = -1.
(0)__+___(1/2)____-___(1)
Вертикальная асимптота: x = 0 и учитывая то, что функция возрастает с 0(не включая) до значения x=1/2, то у функции наименьшего значения нет.
2) Если 1 < x ≤ 2, то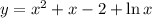 - возрастает на промежутке x > 1. Но на промежутке x ∈ (1; 2] будет наибольшее значение функции в точке x = 2 и равно оно
- возрастает на промежутке x > 1. Но на промежутке x ∈ (1; 2] будет наибольшее значение функции в точке x = 2 и равно оно 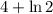 . Наименьшего значения функции не существует.
. Наименьшего значения функции не существует.