Наибольшее значение функции достигается при наибольшем значении квадратного трехчлена, графиком которого является парабола с ветвями вниз. Её наибольшее значение находится при вершине, найдем её координаты:
Заметим что у квадратной функции f(x)= 119 - 10x - x^2 ветви параболы наклонены вниз(т.к -x^2), то есть наибольшее значение данной функции достигается в ее вершины, найдем ее по формуле -b/2a :
ответ:21
Объяснение:
Наибольшее значение функции достигается при наибольшем значении квадратного трехчлена, графиком которого является парабола с ветвями вниз. Её наибольшее значение находится при вершине, найдем её координаты:
Заметим что у квадратной функции f(x)= 119 - 10x - x^2 ветви параболы наклонены вниз(т.к -x^2), то есть наибольшее значение данной функции достигается в ее вершины, найдем ее по формуле -b/2a :
Подставим данное значение в функцию :
То есть наибольшее значение функции =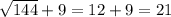
ответ : 21