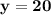Точки экстремума функции :
Знаки производной функции y'
[-4,5] ++++++++ [-4] ----------- [0] ---------> x
Точка x=-4 - точка максимума, так как производная меняет знак с плюса на минус.
ответ : наибольшее значение функции
Точки экстремума функции :
Знаки производной функции y'
[-4,5] ++++++++ [-4] ----------- [0] ---------> x
Точка x=-4 - точка максимума, так как производная меняет знак с плюса на минус.
ответ : наибольшее значение функции