Смотрим на основание логарифма. Оно больше единицы, поэтому функция y=log4(x) возрастает. Это значит, что чем больше x, тем больше значение функции. Но у нас не x, а квадратичная функция, что стоит под логарифмом (называется подлогарифмическое выражение). У этой функции имеется всего лишь одно максимальное значение (вспоминаем график квадратичной функции: если ветви винз, то максимальное значение будет в вершине, а у нас как раз ветви направлены вниз). Собственно, нам осталось найти координату y вершины параболы y=-36-20x-x^2.
.
Теперь найдем вторую координату вершины, подставив это число в функцию.
.
Мы нашли такое число, больше которого логарифм не поднимется. Вычислим значение логарифма: . Значит, максимальное значение исходной функции:
Смотрим на основание логарифма. Оно больше единицы, поэтому функция y=log4(x) возрастает. Это значит, что чем больше x, тем больше значение функции. Но у нас не x, а квадратичная функция, что стоит под логарифмом (называется подлогарифмическое выражение). У этой функции имеется всего лишь одно максимальное значение (вспоминаем график квадратичной функции: если ветви винз, то максимальное значение будет в вершине, а у нас как раз ветви направлены вниз). Собственно, нам осталось найти координату y вершины параболы y=-36-20x-x^2.
 .
.
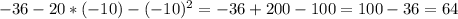 .
.
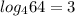 . Значит, максимальное значение исходной функции:
. Значит, максимальное значение исходной функции:
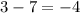 - ответ.
- ответ.
Теперь найдем вторую координату вершины, подставив это число в функцию.
Мы нашли такое число, больше которого логарифм не поднимется. Вычислим значение логарифма: